Câu hỏi:
2 năm trước
Cho hai đường tròn \(\left( {O;10cm} \right)\) và \(\left( {O';5cm} \right)\) cắt nhau tại \(A\) và \(B\) . Tính đoạn nối tâm \(OO'\), biết rằng \(AB = 8\,cm\) và \(O\) và \(O'\) nằm cùng phía đối với \(AB\) . (làm tròn đến chữ số thập phân thứ nhất)
Trả lời bởi giáo viên
Đáp án đúng: d
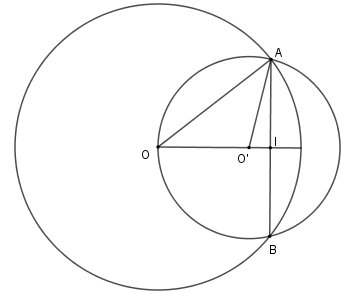
Ta có: \(AI = \dfrac{1}{2}AB = 4\,cm\)
Theo định lý Pytago ta có
\(O{I^2} = O{A^2}-A{I^2} = {10^2} - {4^2} = 84\) \( \Rightarrow \) \(OI = 2\sqrt {21} \) và \(O'I = \sqrt {O'{A^2} - I{A^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Do đó: \(OO' = OI-O'I = 2\sqrt {21} -3 \approx 6,2\left( {cm} \right)\) .
Hướng dẫn giải:
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và định lý Pytago
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
