Khoảng cách giữa hai đường thẳng chéo nhau
Kỳ thi ĐGNL ĐHQG Hà Nội
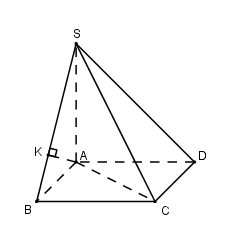
Cho hình chóp $S.ABCD $ có đáy $ABCD$ là hình vuông với \(AC = \dfrac{{a\sqrt 2 }}{2}\). Cạnh bên $SA$ vuông góc với đáy, $SB$ hợp với đáy góc \({60^0}\). Tính khoảng cách $d$ giữa hai đường thẳng $AD$ và $SC.$
Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\)
Tam giác $ABC$ vuông cân tại $B$ nên \(AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{a}{2}\)
Xét tam giác vuông $SAB $ có : \(SA = AB.\tan {60^0} = \dfrac{a}{2}.\sqrt 3 = \dfrac{{a\sqrt 3 }}{2}\)
Ta có \(d\left( {AD;SC} \right) = d\left( {AD;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
Kẻ \(AK \bot SB\).
Do \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\), mà \(AK \bot SB\) nên \(AK \bot \left( {SBC} \right)\)
Khi đó
\(d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{2}}}{{\sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} }} = \dfrac{{a\sqrt 3 }}{4}\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,$ cạnh bằng \(2\). Đường thẳng $SO$ vuông góc với mặt phẳng đáy $(ABCD)$ và $SO = \sqrt 3 $. Tính khoảng cách $d$ giữa hai đường thẳng $SA$ và $BD.$
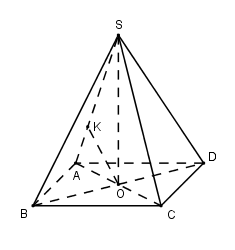
Ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).
Trong (SAC) kẻ \(OK \bot SA\,\,\left( 1 \right)\) ta có : \(OK \subset \left( {SAC} \right) \Rightarrow OK \bot BD\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có $OK$ là đường vuông góc chung của $SA$ và $BD.$ Khi đó $d\left( {SA;BD} \right) = OK = \dfrac{{SO.OA}}{{\sqrt {S{O^2} + O{A^2}} }} = \dfrac{{\sqrt 3 .\dfrac{{2\sqrt 2 }}{2}}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{2\sqrt 2 }}{2}} \right)}^2}} }} = \dfrac{{\sqrt {30} }}{5}.$
Cho hình lăng trụ $ABC.A’B’C’$ có đáy là tam giác đều cạnh có độ dài bằng $2a.$ Hình chiếu vuông góc của $A’$ lên mặt phẳng $(ABC)$ trùng với trung điểm $H$ của $BC.$ Tính khoảng cách $d$ giữa hai đường thẳng $BB’$ và $A’H.$
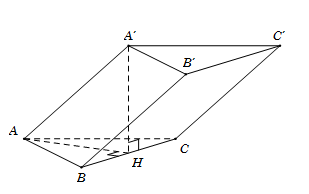
Do \(BB'\parallel AA'\) nên \(d\left( {BB';A'H} \right) = d\left( {BB';\left( {AA'H} \right)} \right) = d\left( {B;\left( {AA'H} \right)} \right).\)
Ta có \(\left\{ \begin{array}{l}BH \bot AH\\BH \bot A'H\end{array} \right. \Rightarrow BH \bot \left( {AA'H} \right)\)
Nên \(d\left( {B;\left( {AA'H} \right)} \right) = BH = \dfrac{{BC}}{2} = a.\)
Vậy khoảng cách \(d\left( {BB';A'H} \right) = a\).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với đáy. Biết rằng đường thẳng $SC$ tạo với đáy một góc ${60^0}.$ Khoảng cách giữa hai đường thẳng $AB$ và $SD$ là
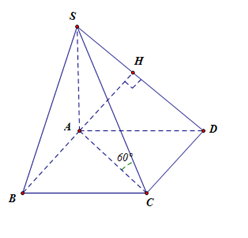
Ta có $AC = a\sqrt 2 .$ Do $SA \bot \left( {ABCD} \right)$ và $SC$ tạo với đáy góc ${60^0}$ nên $\widehat {SCA} = {60^0}$.
Khi đó $SA = AC\tan {60^0} = a\sqrt 6 $. Do $\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)$.
Trong (SAD) dựng $AH \bot SD\,\,\left( 1 \right)$ suy ra \(AB \bot AH\,\,\left( 2 \right)\) là đoạn vuông góc chung $AB$ và $SD$.
Ta có $AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{a\sqrt 6 .a}}{{\sqrt {6{a^2} + {a^2}} }} = \dfrac{{a\sqrt {42} }}{7}$
Vậy khoảng cách $d\left( {AB;SD} \right) = \dfrac{{a\sqrt {42} }}{7}.$
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $A,$ tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng $SA$ và $BC.$
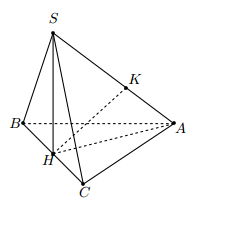
Gọi $H$ là trung điểm của $BC$ khi đó $SH \bot BC$.
Mặt khác $\left( {SBC} \right) \bot \left( {ABC} \right)$ do đó $SH \bot \left( {ABC} \right)$.
Ta có $SH = \dfrac{{a\sqrt 3 }}{2}$ và $AB = AC = \dfrac{a}{{\sqrt 2 }};AH = \dfrac{{BC}}{2} = \dfrac{a}{2}$.
Do $\left\{ \begin{array}{l}BC \bot AH\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHA} \right).$
Dựng $HK \bot SA$ khi đó $HK$ là đoạn vuông góc chung của $BC$ và $SA$.
Lại có $HK = \dfrac{{SH.AH}}{{\sqrt {S{H^2} + H{A^2}} }} = \dfrac{{a\sqrt 3 }}{4}$. Vậy $d\left( {SA;BC} \right) = \dfrac{{a\sqrt 3 }}{4}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,$ cạnh bên $SA$ vuông góc với mặt phẳng đáy. Biết mặt phẳng $(SBC)$ tạo với đáy một góc ${60^0}$ và $M$ là trung điểm của $SD.$ Tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $CM.$
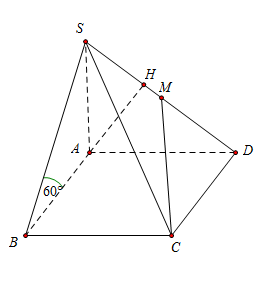
Ta có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) $
$\Rightarrow \widehat {SBA}$ là góc giữa $2$ mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$
Ta có $SA = AB\tan \widehat {SBA} = a\sqrt 3 $.
Do $AB||CD$ do đó $d\left( {AB;CM} \right) = d\left( {AB;\left( {CMD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)$
Dựng \(AH \bot SD\,\,\,\left( 1 \right)\) ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\,\,\left( 2 \right).\)
Từ (1) và (2) \( \Rightarrow AH \bot \left( {SCD} \right)\),
khi đó $d\left( {A;\left( {SCD} \right)} \right) = AH$
Lại có $AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }}$
$= \dfrac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2}.$
Do đó $d = \dfrac{{a\sqrt 3 }}{2}.$
Cho hình chóp $S.ABC$ có đáy $ABCD$ là hình vuông cạnh $a,$ tâm $O.$ Cạnh bên $SA = 2a$ và vuông góc với mặt đáy $(ABCD).$ Gọi $H$ và $K$ lần lượt là trung điểm của cạnh $BC$ và $CD.$ Tính khoảng cách giữa hai đường thẳng $HK$ và $SD.$
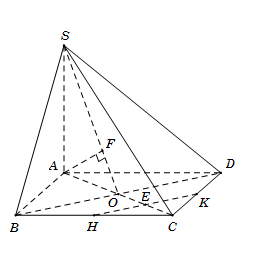
Gọi \(E = HK \cap AC.\) Do \(HK\parallel BD\) nên suy ra
\(d\left( {HK;SD} \right) = d\left( {HK;\left( {SBD} \right)} \right) = d\left( {E;\left( {SBD} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBD} \right)} \right)\) (vì $OE = \dfrac{1}{2}AO$)
Kẻ $AF \bot SO\,\,\left( 1 \right)$ ta có:
\(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AF\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AF \bot \left( {SBD} \right)\), khi đó
\(d\left( {A;\left( {SBD} \right)} \right) = AF = \dfrac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \dfrac{{2a.\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \dfrac{{{a^2}}}{2}} }} = \dfrac{{2a}}{3}.\)
Vậy khoảng cách \(d\left( {HK;SD} \right) = \dfrac{1}{2}AF = \dfrac{a}{3}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,$ cạnh bằng $4a.$ Cạnh bên $SA = 2a.$ Hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(ABCD)$ là trung điểm của $H$ của đoạn thẳng $AO.$ Tính khoảng cách $d$ giữa các đường thẳng $SD$ và $AB.$
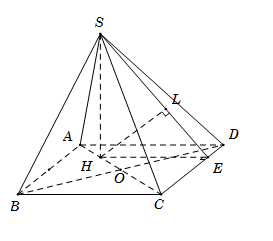
Do \(AB\parallel CD\) nên \(d\left( {SD;AB} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right) = \dfrac{4}{3}d\left( {H;\left( {SCD} \right)} \right).\)
(Do \(AH \cap \left( {SCD} \right) = C \) \(\Rightarrow \dfrac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{AC}}{{HC}} = \dfrac{4}{3} \) \( \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = \dfrac{4}{3}d\left( {H;\left( {SCD} \right)} \right)\))
Kẻ \(HE \bot CD\), kẻ \(HL \bot SE\,\,\left( 1 \right)\) ta có:
\(\left\{ \begin{array}{l}CD \bot SH\\CD \bot HE\end{array} \right. \Rightarrow CD \bot \left( {SHE} \right) \Rightarrow CD \bot HL\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow HL \bot \left( {SCD} \right)\)
\(\Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HL\)
Tính được \(SH = \sqrt {S{A^2} - A{H^2}} = a\sqrt 2 \), \(HE = \dfrac{3}{4}AD = 3a.\)
Khi đó \(d\left( {H;\left( {SCD} \right)} \right) = HL = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{3a\sqrt 2 }}{{\sqrt {11} }}.\)
Vậy \(d\left( {SD;AB} \right) = \dfrac{4}{3}HL = \dfrac{{4a\sqrt {22} }}{{11}}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,$ tam giác $SAD $ đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách $d$ giữa hai đường thẳng $SA$ và $BD.$
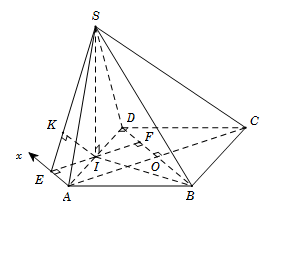
Gọi $I$ là trung điểm của $AD$ nên suy ra $SI \bot AD \Rightarrow SI \bot \left( {ABCD} \right)$ và \(SI = \dfrac{{a\sqrt 3 }}{2}\)
Kẻ \(Ax\parallel BD\). Do đó \(d\left( {BD;SA} \right) = d\left( {BD;\left( {SAx} \right)} \right) = d\left( {D;\left( {SAx} \right)} \right) = 2d\left( {I;\left( {SAx} \right)} \right)\)
(vì \(DI \cap \left( {SAx} \right) = A\) và \(IA = \dfrac{1}{2}DA\))
Kẻ \(IE \bot Ax\), kẻ \(IK \bot SE\,\,\left( 1 \right)\) ta có:
\(\left\{ \begin{array}{l}Ax \bot SI\\Ax \bot IE\end{array} \right. \Rightarrow Ax \bot \left( {SIE} \right) \Rightarrow Ax \bot IK\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow IK \bot \left( {SAx} \right)\). Khi đó \(d\left( {I;\left( {SAx} \right)} \right) = IK\)
Gọi $F$ là hình chiếu của \(I\) trên \(BD\), ta dễ dàng chứng minh được \(\Delta IAE = \Delta IDF\left( {ch - gn} \right) \) \(\Rightarrow IE = IF = \dfrac{{AO}}{2} = \dfrac{{a\sqrt 2 }}{4}\)
Tam giác vuông \(SIE\), có \(IK = \dfrac{{SI.IE}}{{\sqrt {S{I^2} + I{E^2}} }} = \dfrac{{a\sqrt {21} }}{{14}}\)
Vậy \(d\left( {BD;SA} \right) = 2IK = \dfrac{{a\sqrt {21} }}{7}.\)
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, gọi $I$ là trung điểm của $AB$. Hình chiếu vuông góc của $S$ trên mặt đáy là trung điểm của $CI.$ Biết chiều cao của khối chóp là $a\sqrt 3 .$ Khoảng cách giữa hai đường thẳng $AB$ và $SC$ là :
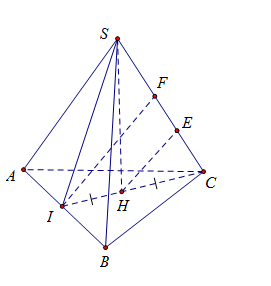
Ta có $\left\{ \begin{array}{l}CI \bot AB\\SH \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SIC} \right)$
Dựng $IF \bot SC\,\,\left( 1 \right)$ khi đó \(IF \subset \left( {SIC} \right) \Rightarrow IF \bot AB\,\,\left( 2 \right)\), do đó $IF$ là đoạn vuông góc chung của $AB$ và $SC$. Dựng $HE \bot SC \Rightarrow HE//IF$ ta có: $HE = \dfrac{1}{2}IF$
Lại có $CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow CH = \dfrac{{a\sqrt 3 }}{4}$
Khi đó
$HE = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + C{H^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 3 }}{4}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{4}} \right)}^2}} }} = \dfrac{{a\sqrt {51} }}{{17}} \Rightarrow IF = \dfrac{{2a\sqrt {51} }}{{17}}$.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Cạnh bên $SA$ vuông góc với mặt phẳng đáy. Biết góc giữa hai mặt phẳng $(SBC)$ và $(ABCD)$ bằng ${60^0}.$ Tính khoảng cách giữa hai đường thẳng $BD$ và $SC.$
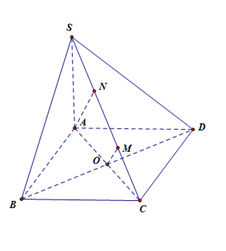
Ta có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)$.
Khi đó $\widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {SBA} = {60^0}$
Suy ra $SA = AB\tan {60^0} = a\sqrt 3 $.
Gọi $O$ là tâm hình vuông $ABCD$ ta có:
$\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)$
Trong $(SAC)$ dựng $OM \bot SC\,\,\left( 1 \right)$ ta có : \(OM \subset \left( {SAC} \right) \Rightarrow OM \bot BD\,\,\left( 2 \right)\) . Từ (1) và (2) suy ra $OM$ là đường vuông góc chung $BD$ và $SC$.
Ta có $\Delta CAS \backsim \Delta CMO\;\;\left( {g - g} \right)$
$\Rightarrow \dfrac{{SC}}{{CO}} = \dfrac{{SA}}{{MO}} \Rightarrow OM = \dfrac{{SA.OC}}{{SC}}$
$ = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{a\sqrt 6 }}{{2\sqrt 5 }} = \dfrac{{a\sqrt {30} }}{{10}}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với mặt phẳng $(ABCD).$ Đường thẳng $SC$ tạo với mặt phẳng đáy góc ${45^0}.$ Khoảng cách giữa hai đường thẳng $SB$ và $AC$ là
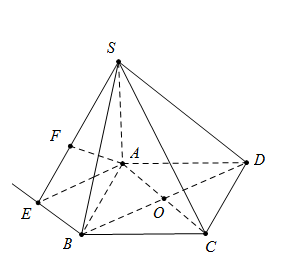
Ta có $AC = a\sqrt 2 ;\widehat {SCA} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = {45^0} \Rightarrow SA = AC = a\sqrt 2 $
Dựng $Bx||AC \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;(SBx)} \right)$
Dựng $AE \bot Bx,\;AF \bot SE\,\,\,\left( 1 \right)$ ta có:
\(\left\{ \begin{array}{l}Bx \bot AE\\Bx \bot SA\end{array} \right. \Rightarrow Bx \bot \left( {SAE} \right) \Rightarrow Bx \bot AF\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AF \bot \left( {SBE} \right)\) \( \Rightarrow d = d\left( {AC;\left( {SBx} \right)} \right) = d\left( {A,\left( {SBx} \right)} \right) = AF\)
Ta có $BE||AC \Rightarrow BE \bot BD$ dễ ràng suy ra $OEBO$ là hình chữ nhật suy ra $AE = OB = \dfrac{{a\sqrt 2 }}{2}.$
Vậy khoảng cách
$d\left( {SB;AC} \right) = \dfrac{{AE.SA}}{{\sqrt {A{E^2} + S{A^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a\sqrt 2 }}{{\sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }} = \dfrac{{a\sqrt {10} }}{5}$.
Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$
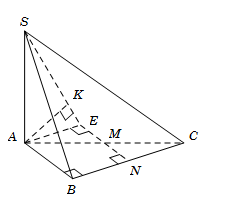
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = 5a\)
Xác định \({60^0} = \widehat {\left( {SC,\left( {ABC} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA}\) và \(SA = AC.\tan \widehat {SCA} = 5a\sqrt 3 .\)
Gọi \(N\) là trung điểm \(BC\), suy ra \(MN\parallel AB\).
Lấy điểm \(E\) đối xứng với \(N\) qua \(M\), suy ra \(ABNE\) là hình chữ nhật.
Do đó $d\left( {AB;SM} \right) = d\left( {AB;\left( {SME} \right)} \right) = d\left( {A;\left( {SME} \right)} \right).$
Kẻ \(AK \bot SE\).
Vì \(ME \bot AE,ME \bot SA\) nên \(ME \bot \left( {SAE} \right) \Rightarrow ME \bot AK\)
Mà \(AK \bot SE\) nên \(AK \bot \left( {SME} \right)\)
Khi đó \(d\left( {A;\left( {SME} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Cạnh bên $SA$ vuông góc với đáy, góc $\widehat {SBD} = {60^0}$. Tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SO.$
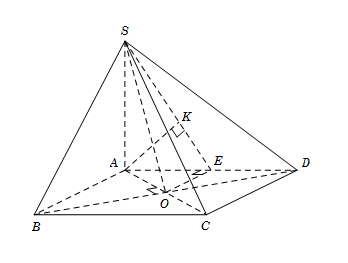
Ta có \(\Delta \,SAB = \Delta \,SAD\) \(\left( {c - g - c} \right)\), suy ra \(SB = SD\).
Mà $\widehat {SBD} = {60^0}$$ \Rightarrow $\(\Delta \,SBD\) đều cạnh \(SB = SD = BD = a\sqrt 2 \).
Tam giác vuông \(SAB\), có \(SA = \sqrt {S{B^2} - A{B^2}} = a\).
Gọi \(E\) là trung điểm \(AD\), suy ra \(OE\parallel AB\) và \(AE \bot OE\).
Do đó \(d\left( {AB;SO} \right) = d\left( {AB;\left( {SOE} \right)} \right) = d\left( {A;\left( {SOE} \right)} \right).\)
Kẻ \(AK \bot SE\,\,\,\left( 1 \right)\)ta có:
\(\left\{ \begin{array}{l}OE \bot AD\\OE \bot SA\end{array} \right. \Rightarrow OE \bot \left( {SAD} \right) \Rightarrow OE \bot AK\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SOE} \right)\)
\( \Rightarrow d\left( {A;\left( {SOE} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{a\sqrt 5 }}{5}\)
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình vuông cạnh bằng \(10\). Cạnh bện $SA$ vuông góc với mặt phẳng $(ABCD)$ và $SC = 10\sqrt 5 $. Gọi $M, N$ lần lượt là trung điểm của $SA$ và $CD.$ Tính khoảng cách giữa BD và MN.
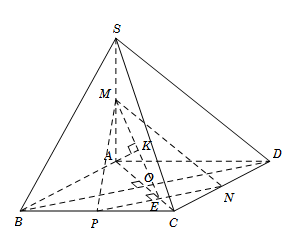
Gọi \(P\) là trung điểm \(BC\) và \(E = NP \cap AC\), suy ra \(PN\parallel BD\) nên \(BD\parallel \left( {MNP} \right)\).
Do đó
\(d\left( {BD;MN} \right) = d\left( {BD;\left( {MNP} \right)} \right) = d\left( {O;\left( {MNP} \right)} \right)\)
Ta có \(PE//BO,P\) là trung điểm của \(BC\) nên \(E\) là trung điểm của \(OC\), do đó \(OE = \dfrac{1}{3}AE\)
Mà \(AO \cap \left( {MNP} \right) = E \Rightarrow d\left( {O;\left( {MNP} \right)} \right) = \dfrac{1}{3}d\left( {A;\left( {MNP} \right)} \right).\)
Kẻ \(AK \bot ME\,\,\left( 1 \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\\NP//BD \Rightarrow NP \bot \left( {SAC} \right) \Rightarrow NP \bot AK\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {MNP} \right)\). Khi đó \(d\left( {A;\left( {MNP} \right)} \right) = AK.\)
Tính được \(SA = \sqrt {S{C^2} - A{C^2}} = 10\sqrt 3 \Rightarrow MA = 5\sqrt 3 ;\,\,AE = \dfrac{3}{4}AC = \dfrac{{15\sqrt 2 }}{2}\)
Tam giác vuông \(MAE\), có \(AK = \dfrac{{MA.AE}}{{\sqrt {M{A^2} + A{E^2}} }} = 3\sqrt 5 .\) Vậy \(d\left( {BD;MN} \right) = \dfrac{1}{3}AK = \sqrt 5 \).
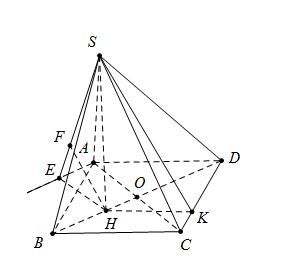
Cho hình chóp $S.ABCD $ có đáy $ABCD$ là hình vuông cạnh $2a.$ Hình chiếu vuông góc của $S$ trên mặt phẳng $(ABCD)$ là điểm $H$ thuộc đoạn $BD$ sao cho $HD = 3HB.$ Biết góc giữa mặt phẳng $(SCD)$ và mặt đáy bằng ${45^0}.$ Khoảng cách giữa hai đường thẳng $SA$ và $BD$ là
Kẻ \(HK \bot CD \Rightarrow CD \bot \left( {SHK} \right)\), do đó góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) là \(\widehat {SKH} = {45^0}\)
Ta có \(\Delta HKD\) vuông cân tại $K$, do vậy \(HK = KD = \dfrac{{3a}}{2} \Rightarrow SH = HK.\tan {45^0} = \dfrac{{3a}}{2}\)
Dựng \(Ax//BD\) ta có \(d\left( {SA,BD} \right) = d\left( {BD,\left( {SAx} \right)} \right) = d\left( {H,\left( {SAx} \right)} \right)\)
Dựng \(HE \bot Ax \Rightarrow HE = OA = a\sqrt 2 \)
Dựng $HF \bot SE\,\,\,\left( 1 \right)$ ta có: \(\left\{ \begin{array}{l}Ax \bot SH\\Ax \bot HE\end{array} \right. \Rightarrow Ax \bot \left( {SHE} \right) \Rightarrow Ax \bot HF\,\,\left( 2 \right)\)
Từ (1) và (2) $ \Rightarrow HF \bot \left( {SAx} \right) \Rightarrow d\left( {H;\left( {SAx} \right)} \right) = HF$
Vậy $HF = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{3a}}{2}.a\sqrt 2 }}{{\sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }} = \dfrac{{3a\sqrt {34} }}{{17}} = d$.
Cho hình lăng trụ $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông cân, $AC = BC = 3a.$ Hình chiếu vuông góc của $B’$ lên mặt đáy trùng với trọng tâm của tam giác $ABC,$ mặt phẳng $(ABB’A’)$ tạo với mặt phẳng $(ABC)$ một góc ${60^0}.$ Tính khoảng cách giữa hai đường thẳng $AB$ và $B’C.$
Gọi \(G\) là trọng tâm tam giác \(ABC\) thì \(B'G \bot \left( {ABC} \right)\)
Dựng \(CI \bot AB\), suy ra $I$ là trung điểm của $AB.$
Ta có: \(\left\{ \begin{array}{l}AB \bot B'G\\AB \bot GI\end{array} \right. \Rightarrow AB \bot \left( {B'GI} \right) \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right)} = \widehat {B'IG} = {60^0}\)
Lại có \(CI = \dfrac{1}{2}AB = \dfrac{{3a\sqrt 2 }}{2} \Rightarrow GI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow B'G = GI.\tan {60^0} = \dfrac{{a\sqrt 6 }}{2}\)
Dựng \(IH \bot B'C\) ta có \(IH \subset \left( {B'IC} \right)\), mà \(AB \bot \left( {B'IC} \right) \Rightarrow IH \bot AB\)
\( \Rightarrow d\left( {AB;B'C} \right) = IH = \dfrac{{B'G.CI}}{{B'C}}\)
Ta có : $B'C = \sqrt {B'{G^2} + G{C^2}} = \sqrt {\dfrac{{3{a^2}}}{2} + 2{a^2}} = \dfrac{{a\sqrt {14} }}{2} \Rightarrow IH = \dfrac{{3a\sqrt {42} }}{{14}}$
Do đó $d = IH = \dfrac{{3a\sqrt {42} }}{{14}}$
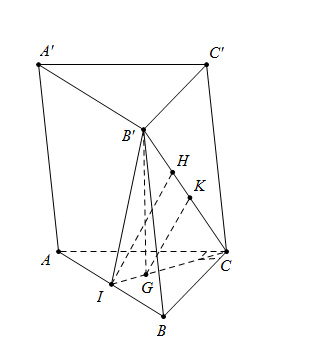
Cho hình lăng trụ đứng $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông, $AB = BC = a,$ \(A'B = a\sqrt 3 \). Gọi $M$ là trung điểm của cạnh $BC.$ Tính khoảng cách giữa hai đường thẳng $AM$ và $B’C.$
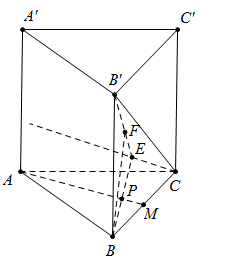
Ta có $AA' = \sqrt {A'{B^2} - A{B^2}} = a\sqrt 2 $.
Dựng $Cx||AM$ khi đó $d\left( {AM;B'C} \right) = d\left( {AM;\left( {B'Cx} \right)} \right)$.
$ = d\left( {M;\left( {B'Cx} \right)} \right) = \dfrac{1}{2}d\left( {B;\left( {B'Cx} \right)} \right)$
(vì \(BM \cap \left( {B'Cx} \right) = C\) và \(M\) là trung điểm của \(BC\))
Dựng $\left\{ \begin{array}{l}BE \bot Cx\\BF \bot B'E\,\,\left( 1 \right)\end{array} \right.$ ta có:
\(\left\{ \begin{array}{l}Cx \bot BE\\Cx \bot BB'\end{array} \right. \Rightarrow Cx \bot \left( {BB'E} \right) \Rightarrow Cx \bot BF\,\,\left( 2 \right)\)
Từ (1) và (2) $ \Rightarrow BF \bot \left( {B'Cx} \right) \Rightarrow d\left( {B;\left( {B'Cx} \right)} \right) = BF$
Gọi \(P = BE \cap AM\), do \(MP//CE,MB = MC\) nên \(PB = PE\)
Mà $BP = \dfrac{{AB.BM}}{{\sqrt {A{B^2} + B{M^2}} }} = \dfrac{{a.\dfrac{a}{2}}}{{\sqrt {{a^2} + \dfrac{{{a^2}}}{4}} }} = \dfrac{a}{{\sqrt 5 }}$
Suy ra $BE = \dfrac{{2a}}{{\sqrt 5 }} \Rightarrow BF = \dfrac{{BE.BB'}}{{\sqrt {B{E^2} + BB{'^2}} }} = \dfrac{{2a}}{{\sqrt 7 }}$
Do đó $d = \dfrac{a}{{\sqrt 7 }}$.
Cho hình lăng trụ đều \(ABC.A'B'C'\) có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là :
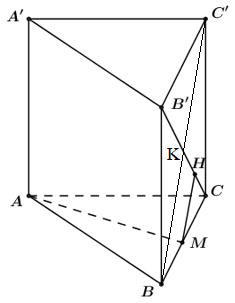
Ta có : \(\left\{ \begin{align} & AM\bot BC \\ & AM\bot BB' \\ \end{align} \right.\Rightarrow AM\bot \left( BCC'B' \right)\)
Trong \(\left( BCC'B' \right)\) kẻ \(MH//BC'\,\,\left( H\in B'C \right)\Rightarrow MH\bot B'C\)
\(MH\subset \left( BCC'B' \right)\Rightarrow AM\bot MH\)
\(\Rightarrow MH\) là đoạn vuông góc chung giữa AM và B’C \(\Rightarrow d\left( AM;B'C \right)=MH\)
Dễ thấy \(MH = \frac{1}{2}BK = \frac{1}{4}B'C = \frac{{a\sqrt 2 }}{4}\) với \(K\) là trung điểm của \(B'C\).
\(\Rightarrow d\left( AM;B'C \right)=\frac{a\sqrt{2}}{4}\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$ với $AB = 2a, AD = DC = a.$ Hai mặt phẳng $(SAB)$ và $(SAD)$ cùng vuông góc với đáy. Góc giữa $SC$ và mặt đáy bằng ${60^0}$. Tính khoảng cách $d$ giữa hai đường thẳng $AC$ và $SB$.
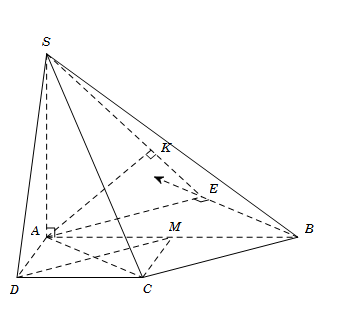
\(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABCD} \right)\)
Xác định
\({60^0} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)} \)
\(= \widehat {\left( {SC;AC} \right)} = \widehat {SCA}\)
và \(SA = AC.\tan \widehat {SCA} \) \(= \sqrt {A{D^2} + C{D^2}} .\tan 60^0 \) \(= a\sqrt 2 .\sqrt 3 = a\sqrt 6. \)
Gọi $M$ là trung điểm $AB$, suy ra $ADCM$ là hình vuông nên $CM = AD = a.$
Xét tam giác $ACB$, ta có trung tuyến \(CM = a = \dfrac{1}{2}AB\) nên tam giác $ACB$ vuông tại $C.$
Lấy điểm $E$ sao cho $ACBE$ là hình chữ nhật, suy ra \(AC\parallel BE\) và E nằm trong (ABCD).
Do đó \(d\left( {AC;SB} \right) = d\left( {AC;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right)\)
Kẻ \(AK \bot SE\,\,\,\left( 1 \right)\) ta có: \(\left\{ \begin{array}{l}BE \bot AE\\BE \bot SA\end{array} \right. \Rightarrow BE \bot \left( {SAE} \right) \Rightarrow BE \bot AK\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBE} \right)\)
Khi đó \(d\left( {A,\left( {SBE} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }}.\)
Ta có: \(AE = BC = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) \(\Rightarrow AK = \dfrac{{a\sqrt 6 .a\sqrt 2 }}{{\sqrt {6{a^2} + 2{a^2}} }} = \dfrac{{a\sqrt 6 }}{2}\)

