Câu hỏi:
2 năm trước
Cho hình lăng trụ $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông cân, $AC = BC = 3a.$ Hình chiếu vuông góc của $B’$ lên mặt đáy trùng với trọng tâm của tam giác $ABC,$ mặt phẳng $(ABB’A’)$ tạo với mặt phẳng $(ABC)$ một góc ${60^0}.$ Tính khoảng cách giữa hai đường thẳng $AB$ và $B’C.$
Trả lời bởi giáo viên
Đáp án đúng: a
Gọi \(G\) là trọng tâm tam giác \(ABC\) thì \(B'G \bot \left( {ABC} \right)\)
Dựng \(CI \bot AB\), suy ra $I$ là trung điểm của $AB.$
Ta có: \(\left\{ \begin{array}{l}AB \bot B'G\\AB \bot GI\end{array} \right. \Rightarrow AB \bot \left( {B'GI} \right) \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right)} = \widehat {B'IG} = {60^0}\)
Lại có \(CI = \dfrac{1}{2}AB = \dfrac{{3a\sqrt 2 }}{2} \Rightarrow GI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow B'G = GI.\tan {60^0} = \dfrac{{a\sqrt 6 }}{2}\)
Dựng \(IH \bot B'C\) ta có \(IH \subset \left( {B'IC} \right)\), mà \(AB \bot \left( {B'IC} \right) \Rightarrow IH \bot AB\)
\( \Rightarrow d\left( {AB;B'C} \right) = IH = \dfrac{{B'G.CI}}{{B'C}}\)
Ta có : $B'C = \sqrt {B'{G^2} + G{C^2}} = \sqrt {\dfrac{{3{a^2}}}{2} + 2{a^2}} = \dfrac{{a\sqrt {14} }}{2} \Rightarrow IH = \dfrac{{3a\sqrt {42} }}{{14}}$
Do đó $d = IH = \dfrac{{3a\sqrt {42} }}{{14}}$
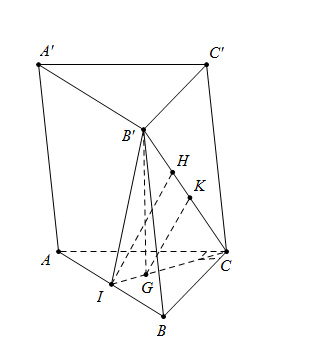
Hướng dẫn giải:
Xác định đường vuông góc chung của $AB$ và $B’C$
