Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,$ cạnh bằng \(2\). Đường thẳng $SO$ vuông góc với mặt phẳng đáy $(ABCD)$ và $SO = \sqrt 3 $. Tính khoảng cách $d$ giữa hai đường thẳng $SA$ và $BD.$
Trả lời bởi giáo viên
Đáp án đúng: b
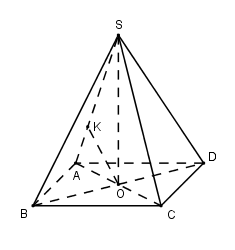
Ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).
Trong (SAC) kẻ \(OK \bot SA\,\,\left( 1 \right)\) ta có : \(OK \subset \left( {SAC} \right) \Rightarrow OK \bot BD\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có $OK$ là đường vuông góc chung của $SA$ và $BD.$ Khi đó $d\left( {SA;BD} \right) = OK = \dfrac{{SO.OA}}{{\sqrt {S{O^2} + O{A^2}} }} = \dfrac{{\sqrt 3 .\dfrac{{2\sqrt 2 }}{2}}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{2\sqrt 2 }}{2}} \right)}^2}} }} = \dfrac{{\sqrt {30} }}{5}.$
Hướng dẫn giải:
+) Dựa vào cách xác định mặt phẳng $(P)$ chứa đường thẳng $SA$ và vuông góc với đường thẳng $BD.$
+) Xác định giao điểm của mặt phẳng $(P)$ với $BD.$
+) Trong $(P)$ từ giao điểm đó kẻ đường thẳng vuông góc với $SA.$
