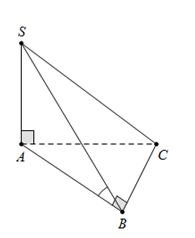
Cho hình chóp $S.ABC$ có đáy \(ABC\). là tam giác vuông tại $B,$ $BC = a$. Cạnh bên $SA = a$ vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ bằng ${45^0}$. Độ dài $AC$ bằng
Ta có $\left( {SBC} \right) \cap \left( {ABC} \right) = BC \Rightarrow BC$ là giao tuyến.
Mặt khác $SA \bot \left( {ABC} \right)$ và $\Delta ABC$ vuông tại $B \Rightarrow AB \bot BC$.
Nên $\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\end{array} \right. \Rightarrow $$BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB$
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SB \bot BC\\\left( {ABC} \right) \supset AB \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {45^0}$
Xét $\Delta SAB$ vuông tại $A$, có $\widehat {SBA} = {45^0} \Rightarrow SA = AB = a$.
Mà $A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 $.
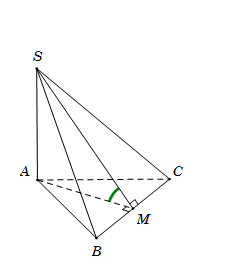
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Cạnh bên $SA = a\sqrt 3 $ và vuông góc với mặt đáy $\left( {ABC} \right)$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$. Mệnh đề nào sau đây đúng?
Gọi \(M\) là trung điểm của $BC$, suy ra $AM \bot BC$
Ta có $\left\{ \begin{array}{l}AM \bot BC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM$
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;AM} \right)} = \widehat {SMA}.$
Tam giác $ABC$ đều cạnh $a$, suy ra trung tuyến $AM = \dfrac{{a\sqrt 3 }}{2}.$
Tam giác vuông $SAM$, có $\sin \widehat {SMA} = \dfrac{{SA}}{{SM}} = \dfrac{{SA}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{{2\sqrt 5 }}{5}.$
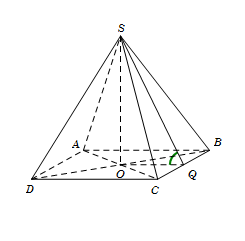
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Đường thẳng $SO$ vuông góc với mặt phẳng đáy $\left( {ABCD} \right)$ và $SO = \dfrac{{a\sqrt 3 }}{2}$. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$.
Gọi \(Q\) là trung điểm \(BC\), suy ra \(OQ \bot BC\).
Ta có $\left\{ \begin{array}{l}BC \bot OQ\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOQ} \right) \Rightarrow BC \bot SQ.$
Do đó
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SQ \bot BC\\\left( {ABCD} \right) \supset OQ \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SQ;OQ} \right)} = \widehat {SQO}.$
Tam giác vuông $SOQ$, có $\tan \widehat {SQO} = \dfrac{{SO}}{{OQ}} = \sqrt 3 \Rightarrow \widehat {SQO} = {60^0}$
Vậy mặt phẳng $\left( {SBC} \right)$ hợp với mặt đáy $\left( {ABCD} \right)$ một góc ${60^0}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$, các cạnh $SA = SB = a,$ $SD = a\sqrt 2 $. Góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right)$ bằng ${90^0}.$ Độ dài đoạn thẳng $BD$
Gọi $I$ là tâm của hình thoi $ABCD$.
Và $H$ là hình chiếu vuông góc của $S$ lên $BD$.
$\widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} = {90^0} \Rightarrow \left( {SBD} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)$.
Khi đó $\left\{ \begin{array}{l}SH \bot AC\\BD \bot AC\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right) \Rightarrow AC \bot SI$.
Mà $I$ là trung điểm của \(AC \Rightarrow \Delta SAC\) cân tại S \( \Rightarrow SA = SB = SC=BC=a\).
\(\Delta SAC = \Delta BAC\left( {c.c.c} \right) \Rightarrow BI = SI = \dfrac{1}{2}BD \Rightarrow \Delta SBD\) vuông tại S
$ \Rightarrow B{D^2} = S{B^2} + S{D^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow BD = a\sqrt 3 $.

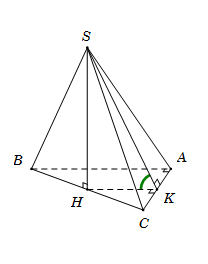
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat {ABC} = {60^0}$, tam giác $SBC$ là tam giác đều có bằng cạnh $2a$ và nằm trong mặt phẳng vuông với đáy. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {ABC} \right)$. Mệnh đề nào sau đây đúng?
Gọi $H$ là trung điểm của \(BC\), suy ra $SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)$.
Gọi $K$ là trung điểm $AC$, suy ra $HK$//$AB$ nên $HK \bot AC$.
Ta có $\left\{ \begin{array}{l}AC \bot HK\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot SK.$
$\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {ABC} \right) = AC\\\left( {SAC} \right) \supset SK \bot AC\\\left( {ABC} \right) \supset HK \bot AC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SK;HK} \right)} = \widehat {SKH}.$
Tam giác vuông $ABC$, có $AB = BC.\cos \widehat {ABC} = a \Rightarrow HK = \dfrac{1}{2}AB = \dfrac{a}{2}.$
Tam giác \(SBC\) đều cạnh \(2a\) có đường cao \(SH = \dfrac{{2a\sqrt 3 }}{2}\)
Tam giác vuông $SHK$, có $\tan \widehat {SKH} = \dfrac{{SH}}{{HK}} = \dfrac{{\dfrac{{2a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = 2\sqrt 3 $.
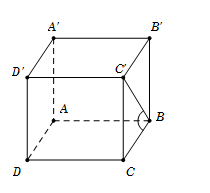
Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có đáy cạnh bằng $a,$ góc giữa hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {ABC'} \right)$ có số đo bằng ${60^0}.$ Độ dài cạnh bên của hình lăng trụ bằng
Vì $ABCD.A'B'C'D'$ là lăng trụ tứ giác đều
$ \Rightarrow \left\{ \begin{array}{l}AB \bot BB'\\AB \bot BC\end{array} \right. \Rightarrow AB \bot \left( {BB'C'B} \right) \Rightarrow AB \bot BC'$
$\left\{ \begin{array}{l}\left( {ABC'} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABC'} \right) \supset BC' \bot AB\\\left( {ABCD} \right) \supset BC \bot AB\end{array} \right. \Rightarrow \widehat {\left( {\left( {ABC'} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {BC';BC} \right)} = \widehat {C'BC} = {60^0}.$
Tam giác $BCC'$ vuông tại $C,$ có $\tan \widehat {C'BC} = \dfrac{{CC'}}{{BC}} \Rightarrow CC' = \tan {60^0}.a = a\sqrt 3 .$
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm $SC$. Tính góc $\varphi $ giữa hai mặt phẳng $\left( {MBD} \right)$ và $\left( {ABCD} \right)$.
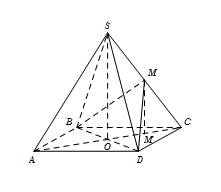
Gọi M’ là trung điểm $OC \Rightarrow MM'\parallel SO \Rightarrow MM' \bot \left( {ABCD} \right).$
Theo công thức diện tích hình chiếu, ta có ${S_{\Delta \,M'BD}} = \cos \varphi .{S_{\Delta \,MBD}}$
$\begin{array}{l} \Rightarrow \cos \varphi = \dfrac{{{S_{\Delta \,M'BD}}}}{{{S_{\Delta \,MBD}}}} = \dfrac{{BD.M'O}}{{BD.MO}} = \dfrac{{M'O}}{{MO}} = \dfrac{{\dfrac{1}{2}OC}}{{\dfrac{1}{2}SA}}\\ = \dfrac{{\sqrt {B{C^2} - O{B^2}} }}{{SA}} = \dfrac{{\sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\end{array}$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $I$, cạnh $a$, góc $\widehat {BAD} = {60^0}$, $SA = SB = SD = \dfrac{{a\sqrt 3 }}{2}$. Gọi \(\varphi \) là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right).$ Mệnh đề nào sau đây đúng?
Từ giả thiết suy ra tam giác $ABD$ đều cạnh $a$.
Gọi $H$ là hình chiếu của $S$ trên mặt phẳng $\left( {ABCD} \right)$.
Do $SA = SB = SD$ nên suy ra $H$ là tâm của tam gác đều $ABD$.
Suy ra $AH = \dfrac{2}{3}AI = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3},HI = \dfrac{1}{3}AI = \dfrac{1}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}$
và $SH = \sqrt {S{A^2} - A{H^2}} = \dfrac{{a\sqrt {15} }}{6}.$
Vì $ABCD$ là hình thoi nên $HI \bot BD$. Tam giác $SBD$ cân tại $S$ nên $SI \bot BD$. Do đó $\widehat {\left( {SBD} \right);\left( {ABCD} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIH}.$.
Trong tam vuông $SHI$, có $\tan \widehat {SIH} = \dfrac{{SH}}{{HI}} = \sqrt 5 .$

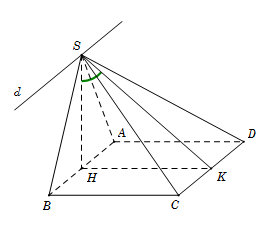
Trong không gian cho tam giác đều $SAB$ và hình vuông $ABCD$ cạnh $a$ nằm trên hai mặt phẳng vuông góc. Gọi $H,$ $K$ lần lượt là trung điểm của $AB$, $CD$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Dễ dàng xác định giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ là đường thẳng $d$ đi qua $S$ và song song với AB và CD.
Trong mặt phẳng $\left( {SAB} \right)$ có $SH \bot AB \Rightarrow SH \bot d.$
Ta có $\left\{ \begin{array}{l}CD \bot HK\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHK} \right) \Rightarrow CD \bot SK \Rightarrow d \bot SK.$
Từ đó suy ra
$\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SCD} \right) = d\\\left( {SAB} \right) \supset SH \bot d\\\left( {SCD} \right) \supset SK \bot d\end{array} \right. \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {SH;SK} \right)} = \widehat {HSK}.$
Trong tam giác vuông $SHK$, có $\tan \widehat {HSK} = \dfrac{{HK}}{{SH}} = \dfrac{a}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{2\sqrt 3 }}{3}.$
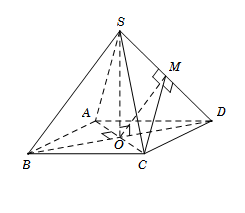
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Gọi $O = AC \cap BD$. Do hình chóp $S.ABCD$ đều nên $SO \bot \left( {ABCD} \right)$.
Gọi $M$ là trung điểm của $SD.$ Tam giác $SCD$ đều nên $CM \bot SD$.
Tam giác $SBD$ có $SB = SD = a,$ $BD = a\sqrt 2 $
Suy ra $\Delta \,SBD$ vuông tại $S \Rightarrow SB \bot SD \Rightarrow OM \bot SD.$
Do đó
$\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {SCD} \right) = SD\\\left( {SBD} \right) \supset OM \bot SD\\\left( {SCD} \right) \supset CM \bot SD\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {OM;CM} \right)} = \widehat {OMC}.$
Ta có $\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow OC \bot OM$.
Tam giác vuông MOC vuông tại O, có $\tan \widehat {CMO} = \dfrac{{OC}}{{OM}} = \dfrac{{\dfrac{1}{2}a\sqrt 2 }}{{\dfrac{1}{2}a}} = \sqrt 2 $.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,$ cạnh bên $SA$ vuông góc với đáy. Gọi $E,\,\,\,F$ lần lượt là trung điểm của cạnh $AB$ và $AC.$ Góc giữa hai mặt phẳng $\left( {SEF} \right)$ và $\left( {SBC} \right)$ là
Gọi $\left( d \right)$ là đường thẳng đi qua $S$ và song song với EF.
Vì EF là đường trung bình tam giác ABC suy ra EF // BC.
Khi đó d // EF // BC$ \Rightarrow \left( {SEF} \right) \cap \left( {SBC} \right) = \left( d \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right).$
Ta có $\left\{ \begin{array}{l}SA \bot BC\,\,\,\,\left( {SA \bot \left( {ABC} \right)} \right)\\AB \bot BC\end{array} \right.$$ \Rightarrow $$BC \bot \left( {SAB} \right) \Rightarrow \left\{ \begin{array}{l}BC \bot SE\\BC \bot SB\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$
Từ $\left( 1 \right),\,\,\left( 2 \right)$ suy ra $\left\{ \begin{array}{l}\left( d \right) \bot SE\\\left( d \right) \bot SB\end{array} \right. \Rightarrow \widehat {\left( {\left( {SEF} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {SE;SB} \right)} = \widehat {BSE}.$

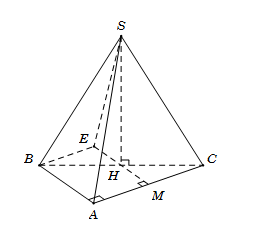
Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a,$ góc giữa mặt bên và mặt đáy bằng ${60^0}.$ Tính độ dài đường cao $SH$ của khối chóp.
Gọi $H$ là chân đường cao kẻ từ đỉnh $S$ xuống mặt phẳng (ABC).
Vì S.ABC là hình chóp đều có SA = SB = SC nên suy ra H chính là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi M là trung điểm của BC, ta có
$\left\{ \begin{array}{l}BC \bot AM\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM$.
Khi đó
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;AM} \right)} = \widehat {SMA} = {60^0}$.
Tam giác ABC đều cạnh a có $AM = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HM = \dfrac{{AM}}{3} = \dfrac{{a\sqrt 3 }}{6}.$
Tam giác AHM vuông tại H, có $SH = \tan {60^0}.\dfrac{{a\sqrt 3 }}{6} = \dfrac{a}{2}.$
Vậy độ dài đường cao $SH = \dfrac{a}{2}.$
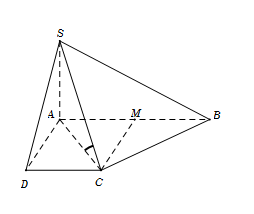
Cho hình chóp $S.ABCD$ có đáy là hình thang vuông $ABCD$ vuông tại $A$ và $D$, $AB = 2a,$ $AD = CD = a$. Cạnh bên $SA = a$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ . Mệnh đề nào sau đây đúng?
Gọi $M$ là trung điểm $AB$ $\, \Rightarrow ADCM$ là hình vuông.
Vì$\,CM = AD = a = \dfrac{{AB}}{2}$. Suy ra tam giác $ACB$ có trung tuyến bằng nửa cạnh đáy nên vuông tại $C$.
Ta có $\left\{ \begin{array}{l}BC \bot SA\\BC \bot AC\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC.$
Do đó :
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SC \bot BC\\\left( {ABCD} \right) \supset AC \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}.$
Tam giác $SAC$ vuông tại $A$$ \Rightarrow \tan \varphi = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{D^2} + C{D^2}} }} = \dfrac{a}{{a\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.$
Cho hình lăng trụ đứng $ABC.A'B'C'$, đáy $ABC$ là tam giác đều $a$. Gọi $I$ là trung điểm của $BC$. Góc giữa hai mặt phẳng $\left( {C'AI} \right)$ và $\left( {ABC} \right)$ bằng ${60^0}$. Độ dài $AA'$ bằng
Ta có $I$ là trung điểm của $BC\,\, \Rightarrow AI \bot BC$
$ABC.A'B'C'$ là lăng trụ đứng $ \Rightarrow C'C \bot \left( {ABC} \right).$
$ \Rightarrow C'C \bot AI$ mà $AI \bot BC \Rightarrow AI \bot \left( {BCC'B'} \right) \Rightarrow AI \bot C'I$
Suy ra
$\left\{ \begin{array}{l}\left( {C'AI} \right) \cap \left( {ABC} \right) = AI\\\left( {C'AI} \right) \supset C'I \bot AI\\\left( {ABC} \right) \supset BC \bot AI\end{array} \right. \Rightarrow \widehat {\left( {\left( {C'AI} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {C'I;BC} \right)} = \widehat {C'IC} = {60^0}$
Xét $\Delta \,C'CI$ vuông tại $C$, có : $\tan \widehat {C'IC} = \dfrac{{CC'}}{{IC}} \Rightarrow CC' = \tan {60^0}.\dfrac{a}{2} = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AA' = \dfrac{{a\sqrt 3 }}{2}$

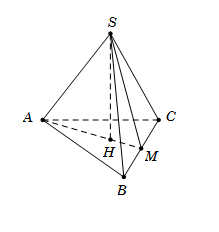
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = AC = a$. Hình chiếu vuông góc $H$ của $S$ trên mặt đáy $\left( {ABC} \right)$ trùng với tâm đường tròn ngoại tiếp tam giác $ABC$ và $SH = \dfrac{{a\sqrt 6 }}{2}$. Gọi $\varphi $ là góc giữa hai đường thẳng $SB$ và $AC$. Mệnh đề nào sau đây đúng?
Gọi $H$ là trung điểm $BC.$ Tam giác $ABC $ vuông tại $A$ nên $H$ trung điểm của $BC.$
Theo giả thiết, ta có $SH \bot \left( {ABC} \right)$
Qua $B$ kẻ $Bx$//$AC$. Khi đó $\widehat {\left( {SB;AC} \right)} = \widehat {\left( {SB;Bx} \right)}$
Kẻ $HE \bot Bx$ tại $E$, cắt $AC$ tại $M$
Suy ra AMEB là hình chữ nhật nên $\left\{ \begin{array}{l}BE = AM = \dfrac{1}{2}AC = \dfrac{a}{2}\\HE = HM = \dfrac{1}{2}AB = \dfrac{a}{2}\end{array} \right.$
Ta có $\left\{ \begin{array}{l}Bx \bot HE\\Bx \bot SH\end{array} \right. \Rightarrow Bx \bot \left( {SHE} \right) \Rightarrow Bx \bot SE$
Tam giác vuông $SEB$ vuông tại $E,$ có $\cot \widehat {SBE} = \dfrac{{BE}}{{SE}} = \dfrac{{AM}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{a}{2}}}{{\sqrt {\dfrac{{6{a^2}}}{4} + \dfrac{{{a^2}}}{4}} }} = \dfrac{{\sqrt 7 }}{7}$
Trong mặt phẳng $\left( P \right)$ cho nửa đường tròn đường kính $AB = 2R$ và điểm $C$ thuộc nửa đường tròn đó sao cho $AC = R$. Trên đường thẳng vuông góc với $\left( P \right)$ tại $A$ lấy điểm $S$ sao cho góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ bằng ${60^0}$. Gọi $H,\,\,K$ lần lượt là hình chiếu của $A$ lên $SB,\,\,SC$. Độ dài cạnh $SA$ tính theo $R$ là
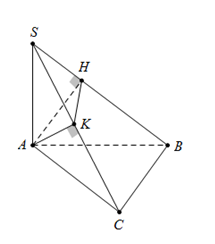
Ta có $\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot AK$.
Do đó $AK \bot \left( {SBC} \right) \Rightarrow AK \bot KH$.
\(\begin{array}{l}\left\{ \begin{array}{l}AH \bot SB\\AK \bot SB\end{array} \right. \Rightarrow SB \bot \left( {AHK} \right) \Rightarrow SB \bot HK\\\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \supset AH \bot SB\\\left( {SAC} \right) \supset HK \bot SB\end{array} \right.\Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {AH;HK} \right)} = \widehat {AHK} = {60^0}\end{array}\)
Xét tam giác AHK vuông tại K có:
$AK = AH.\sin {60^0} \Leftrightarrow A{K^2} = \dfrac{3}{4}A{H^2} \Leftrightarrow \dfrac{3}{4}\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}}$.
Đặt SA = a, áp dụng hệ thức lượng, ta được
- $\dfrac{1}{{A{K^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{R^2}}}$
- $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{R^2}}}$
Suy ra $\dfrac{3}{4}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{R^2}}}} \right) = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{R^2}}} \Leftrightarrow \dfrac{1}{4}\dfrac{1}{{{a^2}}} = \dfrac{1}{2}\dfrac{1}{{{R^2}}} \Leftrightarrow {a^2} = \dfrac{{{R^2}}}{2} \Leftrightarrow a = \dfrac{R}{{\sqrt 2 }}$.
Trong mặt phẳng $\left( P \right)$ cho tam giác đều $ABC$ cạnh $a$. Trên các đường thẳng vuông góc với mặt phẳng $\left( P \right)$ tại $B$ và $C$ lấy điểm $D,\,\,E$ cùng phía so với $\left( P \right)$ sao cho $BD = \dfrac{{a\sqrt 3 }}{2}$ và $CE = a\sqrt 3 $. Tính góc giữa hai mặt phẳng $\left( {ADE} \right)$ và $\left( {ABC} \right)$.
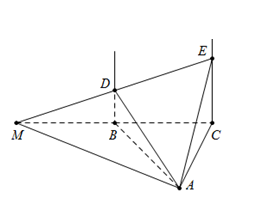
Vẽ $BC \cap DE = M$$ \Rightarrow \left( {ADE} \right) \cap \left( {ABC} \right) = AM$.
Ta có $BD$//$CE \Rightarrow \dfrac{{BD}}{{CE}} = \dfrac{{MB}}{{MC}} = \dfrac{1}{2} $$\Rightarrow BM = BC = BA$.
Suy ra $\Delta AMC$ vuông tại $A$ $ \Rightarrow AM \bot AC$.
$ \Rightarrow \left\{ \begin{array}{l}AM \bot AC\\AM \bot EC\end{array} \right. \Rightarrow AM \bot \left( {ACE} \right) \Rightarrow AM \bot AE \Rightarrow \Delta AME$ vuông tại $A$.
Mặt khác ta có: $\left\{ \begin{array}{l}\left( {ADE} \right) \cap \left( {ABC} \right) = AM\\\left( {ADE} \right) \supset AE \bot AM\\\left( {ABC} \right) \supset AC \bot AM\end{array} \right. $$\Rightarrow \widehat {\left( {\left( {ADE} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {AE;AC} \right)} = \widehat {EAC}$.
Xét $\Delta AEC$ vuông tại C, có $\tan \widehat {EAC} = \dfrac{{EC}}{{AC}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 $$ \Rightarrow \widehat {EAC} = {60^0}$.
Cho hai tam giác $ACD$ và $BCD$ nằm trên hai mặt phẳng vuông góc với nhau và $AC = AD = BC = BD = a,\,\,\,CD = 2x.$ Với giá trị nào của $x$ thì hai mặt phẳng $\left( {ABC} \right)$ và $\left( {ABD} \right)$ vuông góc.
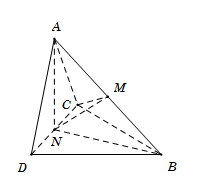
Gọi $M, N$ lần lượt là trung điểm của $AB, CD.$
Ta có $AN \bot CD$ mà $\left( {ACD} \right) \bot \left( {BCD} \right)$
$ \Rightarrow AN \bot \left( {BCD} \right) \Rightarrow AN \bot BN \Rightarrow \Delta ANB$ vuông tại N \( \Rightarrow NM = \dfrac{{AB}}{2}\,\,\left( 1 \right)\)
Tam giác $ABC$ cân tại $C,$ có $M$ là trung điểm của $AB$ $ \Rightarrow CM \bot AB.$
Giả sử $\left( {ABC} \right) \bot \left( {ABD} \right)$ mà $CM \bot AB$$ \Rightarrow CM \bot \left( {ABD} \right) \Rightarrow CM \bot DM.$
Khi đó, $\Delta \,MCD$ vuông tại $M$. Ta có \(\Delta ABC = \Delta ABD\,\,\left( {c.c.c} \right) \Rightarrow CM = DM \Rightarrow \Delta MCD\) vuông cân tại M.
$ \Rightarrow \,\,MN = \dfrac{{CD}}{2}\,\,\,\left( 2 \right)$.
Từ (1) và (2) $ \Rightarrow AB = CD = 2x$
Lại có $\Delta ACD = \Delta BCD\,\,\left( {c.c.c} \right) \Rightarrow AN = BN = \sqrt {A{C^2} - C{N^2}} = \sqrt {{a^2} - {x^2}} ,$ mà $A{B^2} = A{N^2} + B{N^2}.$
Suy ra $2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2} \Leftrightarrow x = \dfrac{{a\sqrt 3 }}{3}.$
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $C$. Gọi $H$ là trung điểm $AB$. Biết rằng $SH$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và $AB = SH = a.$ Tính cosin của góc $\alpha $ tọa bởi hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$.
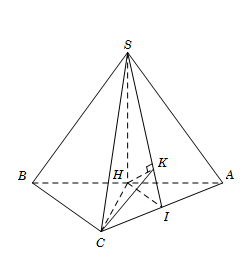
Ta có $SH \bot \left( {ABC} \right) \Rightarrow SH \bot CH$ (1)
Tam giác ABC cân tại C nên $CH \bot AB$ (2)
Từ (1) và (2), suy ra $CH \bot \left( {SAB} \right)$
Gọi I là trung điểm $AC$ $\Rightarrow \,\,HI//BC\xrightarrow{BC\,\bot \,\,AC}HI\bot AC$ (3)
Mặt khác $AC \bot SH$ (do $SH \bot \left( {ABC} \right)$) (4)
Từ (3) và (4), suy ra $AC \bot \left( {SHI} \right)$
Kẻ $HK \bot SI{\rm{ }}\,\left( {K \in SI} \right)$ (5)
Từ $AC \bot \left( {SHI} \right) \Rightarrow AC \bot HK$ (6)
Từ (5) và (6), suy ra $HK \bot \left( {SAC} \right)$
Vì $\left\{ \begin{array}{l}HK \bot \left( {SAC} \right)\\HC \bot \left( {SAB} \right)\end{array} \right.$ nên góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SAB} \right)$ bằng góc giữa hai đường thẳng $HK$ và $HC$
Ta có \(HK \bot \left( {SAC} \right) \Rightarrow HK \bot CK \Rightarrow \Delta CHK\) vuông tại $K.$
Do đó góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SAB} \right)$ là \(\widehat {CHK}\)
Có $CH = \dfrac{1}{2}AB = \dfrac{a}{2}$; $\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{1}{2}.\dfrac{a}{{\sqrt 2 }}} \right)}^2}}} \Rightarrow HK = \dfrac{a}{3}$
Do đó $\cos \widehat {CHK} = \dfrac{{HK}}{{CH}} = \dfrac{{\dfrac{a}{3}}}{{\dfrac{a}{2}}} = \dfrac{2}{3}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA = x$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Xác định $x$ để hai mặt phẳng $\left( {SBC} \right)$ và $\left( {SCD} \right)$ tạo với nhau một góc ${60^0}.$
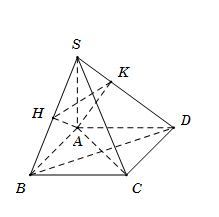
Từ $A$ kẻ $AH$ vuông góc với $SB\,\,\,\,\left( {H \in SB} \right).$
Ta có $\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH$ mà $AH \bot SB$ suy ra $AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$
Từ A kẻ AK vuông góc với $SD\,\,\,\left( {K \in SD} \right),$ tương tự, chứng minh được $AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC$
Khi đó $SC \bot \left( {AHK} \right)$ suy ra
$\widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK} = {60^0}.$
Lại có $\Delta \,SAB = \Delta \,SAD\,\,\left( {c.g.c} \right) \Rightarrow AH = AK$ mà $\widehat {HAK} = {60^0}$ suy ra tam giác AHK đều.
Tam giác SAB vuông tại A có $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{a^2}}} \Rightarrow AH = \dfrac{{xa}}{{\sqrt {{x^2} + {a^2}} }} = AK = HK$
Suy ra $SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{x^2} - \dfrac{{{x^2}{a^2}}}{{{x^2} + {a^2}}}} = \dfrac{{{x^2}}}{{\sqrt {{x^2} + {a^2}} }} \Rightarrow \dfrac{{SH}}{{SB}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}.$
Tương tự ta chứng minh được \(\dfrac{{SK}}{{SC}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}\)
$ \Rightarrow HK$//$BD$ suy ra $\dfrac{{SH}}{{SB}} = \dfrac{{HK}}{{BD}} \Leftrightarrow \dfrac{{{x^2}}}{{{x^2} + {a^2}}} = \dfrac{{xa}}{{\sqrt {{x^2} + {a^2}} .a\sqrt 2 }} \Leftrightarrow \dfrac{x}{{\sqrt {{x^2} + {a^2}} }} = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow 2{x^2} = {x^2} + {a^2} \Rightarrow x = a.$

