Câu hỏi:
2 năm trước
Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có đáy cạnh bằng $a,$ góc giữa hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {ABC'} \right)$ có số đo bằng ${60^0}.$ Độ dài cạnh bên của hình lăng trụ bằng
Trả lời bởi giáo viên
Đáp án đúng: c
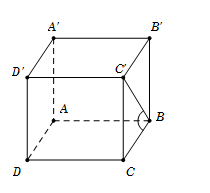
Vì $ABCD.A'B'C'D'$ là lăng trụ tứ giác đều
$ \Rightarrow \left\{ \begin{array}{l}AB \bot BB'\\AB \bot BC\end{array} \right. \Rightarrow AB \bot \left( {BB'C'B} \right) \Rightarrow AB \bot BC'$
$\left\{ \begin{array}{l}\left( {ABC'} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABC'} \right) \supset BC' \bot AB\\\left( {ABCD} \right) \supset BC \bot AB\end{array} \right. \Rightarrow \widehat {\left( {\left( {ABC'} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {BC';BC} \right)} = \widehat {C'BC} = {60^0}.$
Tam giác $BCC'$ vuông tại $C,$ có $\tan \widehat {C'BC} = \dfrac{{CC'}}{{BC}} \Rightarrow CC' = \tan {60^0}.a = a\sqrt 3 .$
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
