Diện tích hình nón, thể tích khối nón

Công thức tính diện tích xung quanh hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là: \({S_{xq}} = \pi rl\)

Áp dụng công thức \({S_{xq}} = \pi rl\) ta được: \({S_{xq}} = \pi .3.4 = 12\pi \left( {c{m^2}} \right)\)

Từ công thức \({S_{xq}} = \pi rl\) ta có: \(l = \dfrac{{{S_{xq}}}}{{\pi r}}\) 

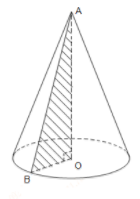
Quan sát hình vẽ ta thấy: \(l = AB,r = OB,h = AO\).

Mà \(A{B^2} = A{O^2} + O{B^2}\) nên \({l^2} = {r^2} + {h^2}\) 

Công thức tính diện tích toàn phần hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là: \({S_{tp}} = \pi rl + \pi {r^2}\)

Trong mặt phẳng \(\left( P \right)\) cho hai đường thẳng \(d,d'\) cắt nhau tại \(O\) và tạo thành góc \(\alpha \left( {{0^0} < \alpha  < {{90}^0}} \right)\). Khi quay mặt phẳng \(\left( P \right)\) xung quanh \(d\) thì đường thẳng \(d'\) sinh ra một mặt được gọi là mặt nón tròn xoay (gọi tắt mặt nón).

Do đó điều kiện để có được mặt nón tròn xoay là góc \({0^0} < \alpha  < {90^0}\).

Áp dụng công thức \({S_{tp}} = \pi rl + \pi {r^2}\) ta được: \({S_{tp}} = \pi rl + \pi {r^2} = \pi .1.2 + \pi {.1^2} = 3\pi \left( {c{m^2}} \right)\)

\(\alpha \) là góc giữa hai đường thẳng \(d,d'\) thì góc \(2\alpha \) là góc ở đỉnh của mặt nón.

Ta có: \({l^2} = {r^2} + {h^2} \Rightarrow l = \sqrt {{r^2} + {h^2}}  = \sqrt {{1^2} + {2^2}}  = \sqrt 5 \)

Do đó \({S_{tp}} = \pi rl + \pi {r^2} = \pi .1.\sqrt 5  + \pi {.1^2} = \left( {1 + \sqrt 5 } \right)\pi \)

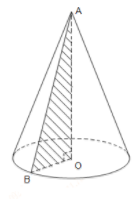
Quan sát hình vẽ ta thấy đường sinh là $AB$ và đường cao $AO$.

Công thức tính thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\)

Ta có: \({l^2} = {r^2} + {h^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} \)

Do đó \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {r^2}\sqrt {{l^2} - {r^2}} \)

Áp dụng công thức tính thể tích khối nón \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.2^2}.3 = 4\pi c{m^3}\) 

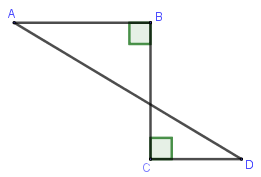
Gọi $O$ là giao điểm của $AD$ và $BC$.

- Quay tam giác vuông \(ABO\) quanh \(BO\) ta được một hình nón.

- Quay tam giác vuông \(DCO\) quanh \(CO\) ta được một hình nón.

Vậy có tất cả hai hình nón được tạo thành.

Ta có: \({l^2} = {r^2} + {h^2} \Rightarrow h = \sqrt {{l^2} - {r^2}}  \Rightarrow V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{3}{S_d}.\sqrt {{l^2} - {r^2}} \)

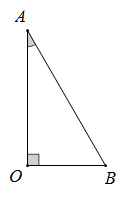
Hình nón thu được có đường sinh $l = AB = a$; bán kính đáy

$r = OB = AB.\sin 30^\circ  = \dfrac{a}{2}$ và diện tích xung quanh là

${S_{xq}} = \pi rl = \dfrac{{\pi {a^2}}}{2}$

$r = \sqrt {\dfrac{{9\pi }}{\pi }}  = 3 \Rightarrow l = 2r = 6;h = \sqrt {{l^2} - {r^2}}  = 3\sqrt 3 $

Độ dài đường cao của hình nón cũng chính là chiều cao của tam giác đều \( \Rightarrow h = \dfrac{{a\sqrt 3 }}{2} = \dfrac{{3\sqrt 3 }}{2}\)

Giả sử thiết diện qua trục của hình nón đã cho là $\Delta ABC$ cân tại $A$ với $A$ là đỉnh nón, $BC$ là đường kính đáy của nón.

Gọi $H$ là tâm đáy nón $ \Rightarrow H$ là trung điểm $BC,AH \bot BC$

Ta có $HB = HC = 1,AH = 2$ . Ta có

$\begin{array}{l}2\varphi  = \angle BAC \Rightarrow \varphi  = \angle HAC\\AC = \sqrt {A{H^2} + H{C^2}}  = \sqrt 5 \\\cos \varphi  = \dfrac{{AH}}{{AC}} = \dfrac{2}{{\sqrt 5 }} = \dfrac{{2\sqrt 5 }}{5}\end{array}$

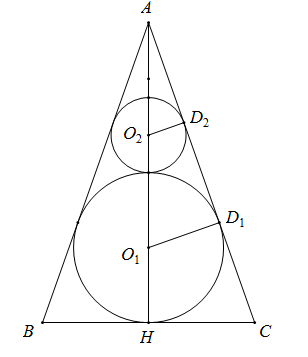
Giả sử thiết diện qua trục của hình nón là $\Delta ABC$ với $A$ là đỉnh nón, $BC$ là đường kính đáy nón.

Gọi $H$ là tâm đường tròn đáy của hình nón, ${O_1},{O_2}$ lần lượt là tâm của mặt cầu lớn và nhỏ, ${D_1},{D_2}$ lần lượt là tiếp điểm của $AC$ với $\left( {{O_1}} \right)$ và $\left( {{O_2}} \right)$.

Vì ${O_1}{D_1}//{O_2}{D_2}$ (cùng vuông góc với $AC$) nên theo hệ thức Ta – let ta có:

\( \Rightarrow \dfrac{{A{O_2}}}{{A{O_1}}} = \dfrac{{{O_2}{D_2}}}{{{O_1}{D_1}}} = \dfrac{a}{{2a}} = \dfrac{1}{2} \)

\(\Rightarrow {O_2}\) là trung điểm của \(A{O_1}\)\( \Rightarrow A{O_1} = 2{O_1}{O_2} = 2\left( {a + 2a} \right) = 6a\)

\( \Rightarrow AH = A{O_1} + {O_1}H = 6a + 2a = 8a\)

Xét tam giác vuông \(A{O_1}{D_1}\) có: \(A{D_1} = \sqrt {A{O_1}^2 - {O_1}{D_1}^2}  = \sqrt {36{a^2} - 4{a^2}}  = 4\sqrt 2 a\)

Dễ thấy:

$\Delta A{O_1}{D_1} \backsim \Delta ACH\,\,\left( {g.g} \right)$$ \Rightarrow \dfrac{{HC}}{{{O_1}{D_1}}} = \dfrac{{AH}}{{A{D_1}}}$$ \Rightarrow HC = \dfrac{{{O_1}{D_1}.AH}}{{A{D_1}}} = \dfrac{{2a.8a}}{{4\sqrt 2 a}} = 2\sqrt 2 a = r$