Thể tích khối hộp

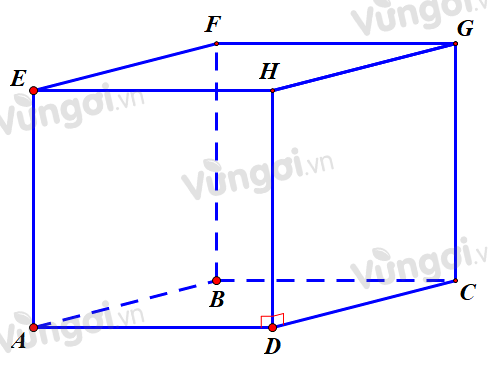
Vì 4 mặt bên của khối hộp là hình vuông nên ta có HD vuông góc với AD và CD

=> cạnh bên HD vuông góc với đáy và chiều cao của khối hộp là HD..

Mặt bên là hình vuông có diện tích bằng 1 nên $HD^2=1=>HD=1$.

Thể tích của khối hộp là $\dfrac{1}{2}.1=\dfrac{1}{2}$

Công thức tính thể tích lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là \(V = Sh\).

Hình hộp chữ nhật có cạnh bên vuông góc với đáy nên cạnh bên chính là đường cao.

Vì hình hộp chữ nhật cũng là hình lăng trụ nên thể tích của khối hộp cũng được tính bởi công thức \(V = Sh\), hay \(V = Sa\).

Thể tích khối lập phương cạnh \(2a\) là: \(V = {\left( {2a} \right)^3} = 8{a^3}\)

Vì \(M \in \left( {A'B'C'} \right) \Rightarrow d\left( {M;\left( {ABC} \right)} \right) = d\left( {\left( {A'B'C'} \right);\left( {ABC} \right)} \right)\)

\( \Rightarrow {V_{M.ABC}} = \dfrac{1}{3}d\left( {M;\left( {ABC} \right)} \right).{S_{ABC}} = \dfrac{1}{3}V\)

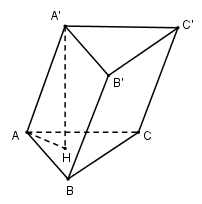
Gọi $H$ là hình chiếu vuông góc của $A'$  trên \(\left( {ABC} \right) \Rightarrow A'H \bot \left( {ABC} \right)\)

\( \Rightarrow AH\) là hình chiếu vuông góc của $AA'$  trên \(\left( {ABC} \right) \Rightarrow \widehat {\left( {AA';\left( {ABC} \right)} \right)} = \widehat {\left( {AA';AH} \right)} = \widehat {A'AH} = {60^0}\)

\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AH \Rightarrow \Delta A'AH\) vuông tại \(H \Rightarrow A'H = AA'.\sin 60 = a\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{2}\)

Tam giác $ABC$ đều cạnh  nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}\sqrt 3 }}{8}\)

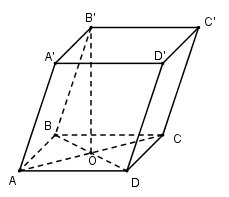
Gọi \(O = AC \cap BD\).

Xét tam giác $ABD$ có $AB = AD = a$ và \(\widehat {BAD} = {60^0} \Rightarrow \Delta ABD\) đều cạnh \(a \Rightarrow BD = a \Rightarrow BO = \dfrac{a}{2}\)

\( \Rightarrow B'O \bot \left( {ABCD} \right) \Rightarrow B'O \bot BO \Rightarrow \Delta BB'O\) vuông tại $O$

$ \Rightarrow B'O = \sqrt {BB{'^2} - B{O^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}$

\({S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{4} \Rightarrow {S_{ABCD}} = 2{S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Vậy \({V_{ABCD.A'B'C'D'}} = B'O.{S_{ABCD}} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}}}{4}\)

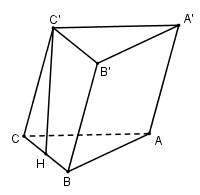
Áp dụng định lí Côsin trong tam giác $ABC$ có: \(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.\cos 120}  \)

$= \sqrt {4{a^2} + {a^2} - 2.2a.a.\dfrac{{ - 1}}{2}}  = a\sqrt 7  \Rightarrow CH = \dfrac{1}{2}BC = \dfrac{{a\sqrt 7 }}{2}$

\(C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot CH \Rightarrow \Delta CC'H\) vuông tại $H$

\( \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}}  = \sqrt {\dfrac{{10{a^2}}}{4} - \dfrac{{7{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

\({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin 120 = \dfrac{1}{2}.2a.a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Vậy \({V_{ABC.A'B'C'}} = C'H.{S_{ABC}} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}}}{4}\)

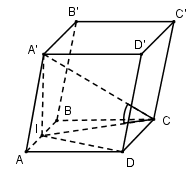
Theo bài ra ta có: $IC$ là hình chiếu vuông góc của $A'C$  trên $\left( {ABCD} \right)$

\( \Rightarrow \widehat {\left( {A'C;\left( {ABCD} \right)} \right)} = \widehat {\left( {A'C;IC} \right)} = \widehat {A'CI} = \alpha \)

Xét tam giác vuông $IBC$ có: \(IC = \sqrt {I{B^2} + B{C^2}}  = \sqrt {\dfrac{{{a^2}}}{4} + {a^2}}  = \dfrac{{a\sqrt 5 }}{2}\)

Xét tam giác vuông $A'IC$  có: \(A'I = IC.\tan \alpha  = \dfrac{{a\sqrt 5 }}{2}.\dfrac{2}{{\sqrt 5 }} = a\)

\({S_{\Delta ICD}} = \dfrac{1}{2}d\left( {I;CD} \right).CD = \dfrac{1}{2}a.a = \dfrac{{{a^2}}}{2}\)

Vậy \({V_{A'.ICD}} = \dfrac{1}{3}A'I.{S_{\Delta ICD}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{6}\)

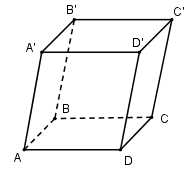
Dựng khối hộp $ABCD.A’B’C’D’$ ta có: \({V_{ABC.A'B'C'}} = \dfrac{1}{2}{V_{ABCD.A'B'C'D'}}\)

Khối hộp \(ABCD.A'B'C'D'\) có hai đáy là $ABB’A’$ và $CDD’C’$

\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABB'A'}}.h\)

Trong đó \(h = d\left( {\left( {ABB'A'} \right);\left( {CDD'C'} \right)} \right) = d\left( {CC';\left( {ABB'A'} \right)} \right) = 7\)

\( \Rightarrow {V_{ABCD.A'B'C'D'}} = 4.7 = 28\)

Vậy \({V_{ABC.A'B'C'}} = \dfrac{1}{2}.28 = 14\)

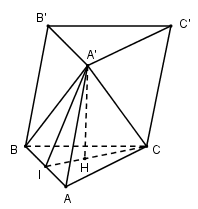
Gọi $H$ là tâm tam giác đều $ABC$ . Vì $A'A = A'B = A'C$ nên hình chóp $A'.ABC$  là đều nên \(A'H \bot \left( {ABC} \right)\)

Gọi $I$ là trung điểm của $AB$.

Vì tam giác $ABC$ đều cạnh $a$ nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\)

Tam giác $A'AB$  cân tại $A'$  nên \(A'I \bot AB \Rightarrow \Delta A'AI\) vuông tại \(I \Rightarrow A'I = \sqrt {AA{'^2} - A{I^2}}  = \sqrt {\dfrac{{7{a^2}}}{{12}} - \dfrac{{{a^2}}}{4}}  = \dfrac{a}{{\sqrt 3 }}\)

\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot HI \Rightarrow \Delta A'HI\) vuông tại \(H \Rightarrow A'H = \sqrt {A'{I^2} - H{I^2}}  = \sqrt {\dfrac{{{a^2}}}{3} - \dfrac{{{a^2}}}{{12}}}  = \dfrac{a}{2}\)

Vì tam giác $ABC$ đều cạnh $a$ nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)

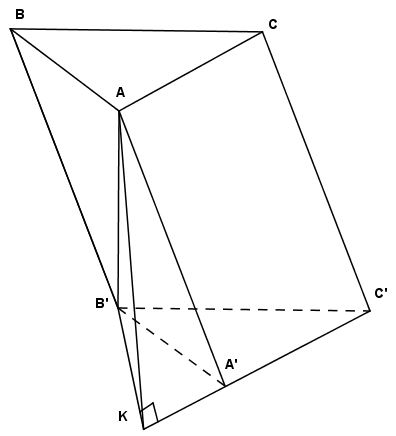
Trong (A’B’C’) kẻ \(B'K \bot A'C'\,\,\left( {K \in A'C'} \right)\)

Ta có:

\(\left. \begin{array}{l}AB' \bot A'C'\left( {AB' \bot \left( {A'B'C'} \right)} \right)\\B'K \bot A'C'\end{array} \right\} \Rightarrow A'C' \bot \left( {AB'K} \right) \Rightarrow A'C' \bot AK\)

\(\left. \begin{array}{l}\left( {AA'C'} \right) \cap \left( {A'B'C'} \right) = A'C'\\\left( {AA'C'} \right) \supset AK \bot A'C'\\\left( {A'B'C'} \right) \supset B'K \bot A'C'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {AA'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AK;B'K} \right)} = \widehat {AKB'} = {30^0}\)

Ta có:

\(\begin{array}{l}{S_{A'B'C'}} = \dfrac{1}{2}A'B'.A'C'.\sin 120 = \dfrac{1}{2}{a^2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{1}{2}B'K.A'C'\\ \Rightarrow B'K = \dfrac{{2{S_{A'B'C'}}}}{{A'C'}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{2}}}{a} = \dfrac{{a\sqrt 3 }}{2}\end{array}\)

\(AB' \bot \left( {A'B'C'} \right) \Rightarrow AB' \bot B'K \Rightarrow \Delta AB'K\) vuông tại B’

$ \Rightarrow AB' = B'K.tan30 = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{3} = \dfrac{a}{2}$

Vậy \({V_{ABC.A'B'C'}} = AB'.{S_{A'B'C'}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)

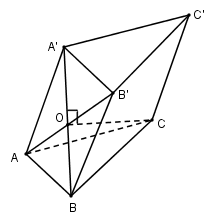
Gọi $O$ là tâm hình bình hành $ABB’A’$. Ta có \(CO \bot \left( {ABB'A'} \right) \Rightarrow CO \bot OA;CO \bot OB\)

\(\Delta COA = \Delta COB\left( {c.g.c} \right) \Rightarrow OA = OB \Rightarrow AB' = A'B \Rightarrow ABB'A'\) là hình chữ nhật.

Lại có \(AB = BB' = a \Rightarrow ABB'A'\) là hình vuông

Khi đó \(OA = OB = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}\)

Xét tam giác vuông $OAC$ có: \(OC = \sqrt {A{C^2} - O{A^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 2 }}{2}\)

\( \Rightarrow {V_{C.A'AB}} = \dfrac{1}{3}OC.{S_{A'AB}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)

Mà ${V_{ABC.A'B'C'}} = {S_{ABC}}.d\left( {A',\left( {ABC} \right)} \right) = 3.\dfrac{1}{3}{S_{ABC}}.d\left( {A',\left( {ABC} \right)} \right) = 3.{V_{A'.ABC}}$

Vậy \({V_{ABC.A'B'C'}} = 3{V_{C.A'AB}} = \dfrac{{{a^3}\sqrt 2 }}{4}\)

Diện tích toàn phần của hình hộp chữ nhật: ${S_{tp}} = {S_{xq}} + 2ab = 2h\left( {a + b} \right) + 2ab.$

Thể tích hình hộp chữ nhật: $V = abh.$

Thể tích của lăng trụ là: $V = {S_d}.h.$

Diện tích toàn phần của khối lập phương: ${S_{tp}} = 6{a^2}.$

Thể tích của khối lập phương: $V = {a^3}.$

Thể tích khối chóp là: $V = \dfrac{1}{3}{S_d}.h.$

Do đó các đáp án B, C, D đúng, chỉ có A sai.

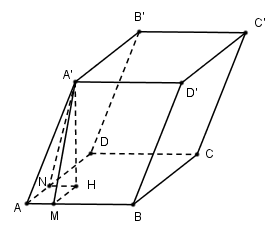
Kẻ \(A'H \bot \left( {ABCD} \right);HM \bot AB;HN \bot AD\)

Ta có: \(\left. \begin{array}{l}A'H \bot AB\\HM \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {A'HM} \right) \Rightarrow AB \bot A'M\)

\(\left. \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABB'A'} \right) \supset A'M \bot AB\\\left( {ABCD} \right) \supset HM \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {A'M;HM} \right)} = \widehat {A'MH} = {45^o}\)

Chứng minh tương tự ta có \(\widehat {A'NH} = {60^0}\)

Đặt \(A'H = x\) khi đó ta có:

\(A'N = \dfrac{x}{{\sin 60}} = \dfrac{{2x}}{{\sqrt 3 }},AN = \sqrt {AA{'^2} - A'{N^2}}  = \sqrt {1 - \dfrac{{4{x^2}}}{3}}  = HM\)

Mà \(HM = x.\cot 45 = x\)

$ \Rightarrow x = \sqrt {1 - \dfrac{{4{x^2}}}{3}}  \Leftrightarrow {x^2} = 1 - \dfrac{{4{x^2}}}{3} \Leftrightarrow \dfrac{{7{x^2}}}{3} = 1 \Rightarrow {x^2} = \dfrac{3}{7} \Rightarrow x = \sqrt {\dfrac{3}{7}} $

\({S_{ABCD}} = \sqrt 3 .\sqrt 7  = \sqrt {21} \)

Vậy \({V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}} = \sqrt {\dfrac{3}{7}} .\sqrt {21}  = 3\)

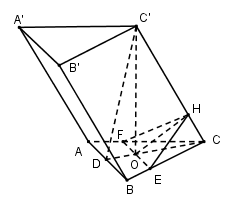
Gọi $D$ là trung điểm của $AB$. Trong $(CC’D)$ kẻ \(OH \bot CC' \Rightarrow OH = a\)

\(\left. \begin{array}{l}CD \bot AB\\C'O \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {CC'D} \right) \Rightarrow AB \bot CC'\)

Trong $(ABC)$, qua $O$ kẻ $EF // AB$ \(\left( {E \in BC;F \in AC} \right)\)

Ta có: \(\left. \begin{array}{l}EF \bot CC'\\OH \bot CC'\end{array} \right\} \Rightarrow CC' \bot \left( {EFH} \right) \Rightarrow CC' \bot HE;CC' \bot HF\)

Ta có: \(\left. \begin{array}{l}\left( {ACC'A'} \right) \cap \left( {BCC'B'} \right) = CC'\\\left( {ACC'A'} \right) \supset HF \bot CC'\\\left( {BCC'B'} \right) \supset HE \bot CC'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ACC'A'} \right);\left( {BCC'B'} \right)} \right)} = \widehat {\left( {HF;HE} \right)} = {90^0} \Rightarrow HE \bot HF\)

\( \Rightarrow \Delta HEF\) vuông tại $H$

\(\Delta HCE = \Delta HCF\left( {c.g.v - c.h} \right) \Rightarrow HE = HF \Rightarrow \Delta HEF\) vuông cân tại H\( \Rightarrow EF = 2HO = 2a\)

Ta có: \(\dfrac{{EF}}{{AB}} = \dfrac{{CO}}{{CD}} = \dfrac{2}{3} \Rightarrow AB = \dfrac{3}{2}EF = \dfrac{3}{2}.2a = 3a\)\( \Rightarrow {S_{\Delta ABC}} = \dfrac{{A{B^2}\sqrt 3 }}{4} = \dfrac{{9{a^2}\sqrt 3 }}{4}\)

\(CD = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{3a\sqrt 3 }}{2} \Rightarrow CO = \dfrac{2}{3}AB = \dfrac{2}{3}.\dfrac{{3a\sqrt 3 }}{2} = a\sqrt 3 \)

\(C'O \bot \left( {ABC} \right) \Rightarrow C'O \bot CO \Rightarrow \Delta CC'O\) vuông tại O

\( \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{C'{O^2}}} + \dfrac{1}{{C{O^2}}} \Rightarrow \dfrac{1}{{C'{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{C{O^2}}} = \dfrac{1}{{{a^2}}} - \dfrac{1}{{3{a^2}}} = \dfrac{2}{{3{a^2}}} \Rightarrow C'O = \dfrac{{\sqrt 6 }}{2}a\)

Vậy ${V_{ABC.A'B'C'}} = C'O.{S_{\Delta ABC}} = \dfrac{{a\sqrt 6 }}{2}.\dfrac{{9{a^2}\sqrt 3 }}{4} = \dfrac{{27{a^3}\sqrt 2 }}{8}$

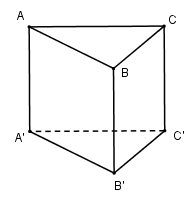
\({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a.a\sqrt 3  = \dfrac{{{a^2}\sqrt 3 }}{2}\) \( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2a.\dfrac{{{a^2}\sqrt 3 }}{2} = {a^3}\sqrt 3 \) 

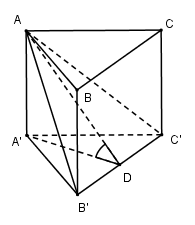
Gọi $D$ là trung điểm của $B'C'$. Vì tam giác \(A'B'C'\) cân tại $A'$  nên \(A'D \bot B'C'\) (trung tuyến đồng thời là đường cao).

Vì $ABC.A'B'C'$ là hình lăng trụ đứng nên $AA' \bot (A'B'C')$.

Ta có: \(\left. \begin{array}{l}A'D \bot B'C'\\AA' \bot B'C'\end{array} \right\} \Rightarrow B'C' \bot \left( {AA'D} \right) \Rightarrow B'C' \bot AD\)

\(\left. \begin{array}{l}\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'\\\left( {AB'C'} \right) \supset AD \bot B'C'\\\left( {A'B'C'} \right) \supset A'D \bot B'C'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AD;A'D} \right)} = \widehat {ADA'} = {60^0}\)

Vì tam giác \(A'B'C'\) cân tại $A'$  nên \(\widehat {DA'C'} = \dfrac{1}{2}\widehat {B'A'C'} = {60^0}\) (trung tuyến đồng thời là phân giác)

Xét tam giác vuông \(A'D'C'\) có: \(A'D = A'C'.cos60 = 2a.\dfrac{1}{2} = a\)

Xét tam giác vuông \(AA'D\) có: \(AA' = A'D.\tan 60 = a.\sqrt 3 \)

\({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC} = \dfrac{1}{2}.2a.2a.\dfrac{{\sqrt 3 }}{2} = {a^2}\sqrt 3 \)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .{a^2}\sqrt 3  = 3{a^3}\)

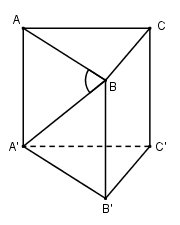
Vì \(AA' \bot \left( {ABC} \right) \Rightarrow AB\) là hình chiếu vuông góc của $A'B$ lên \( (ABC)\Rightarrow \widehat {\left( {A'B;\left( {ABC} \right)} \right)} = \widehat {\left( {A'B;AB} \right)} = \widehat {A'BA} = {30^0}\)

 Xét tam giác vuông $ABC$ có: \(AB = BC.\tan 60 = a\sqrt 3 \)

\(AA' \bot \left( {ABC} \right) \supset AB \Rightarrow AA' \bot AB \Rightarrow \Delta ABA'\) vuông tại $A$ \( \Rightarrow AA' = AB.\tan \widehat {A'BA} = a\sqrt 3 .\tan 30 = a\sqrt 3 .\dfrac{1}{{\sqrt 3 }} = a\)

\({S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{2}\)

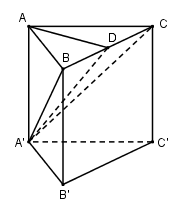
Gọi D là trung điểm của BC ta có:

Tam giác ABC đều nên \(AD \bot BC\) và $AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot BC$

\( \Rightarrow BC \bot \left( {AA'D} \right) \Rightarrow BC \bot A'D \Rightarrow \Delta A'BC\)cân tại A’

 Tam giác ABC đều cạnh \(a = 4 \Rightarrow AD = \dfrac{{4\sqrt 3 }}{2} = 2\sqrt 3 \)

\({S_{\Delta A'BC}} = \dfrac{1}{2}A'D.BC \Rightarrow A'D = \dfrac{{2{S_{\Delta A'BC}}}}{{BC}} = \dfrac{{2.8}}{4} = 4\)

Xét tam giác vuông  AA’D có: \(AA' = \sqrt {A'{D^2} - A{D^2}}  = \sqrt {16 - 12}  = 2\)

\({S_{ABC}} = \dfrac{{{4^2}\sqrt 3 }}{4} = 4\sqrt 3 \)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2.4\sqrt 3  = 8\sqrt 3 \)