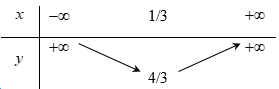
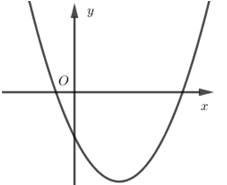
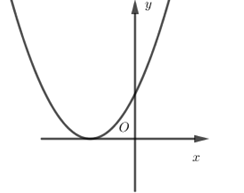
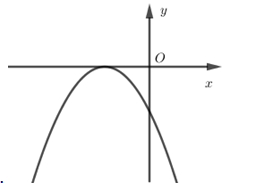
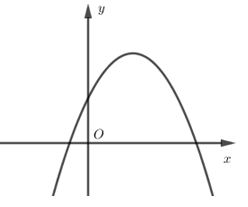
Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol \(y = - 2{x^2} + 5x + 3.\)
Ta có:
\(\dfrac{{ - b}}{{2a}} = \dfrac{{ - 5}}{{2.( - 2)}} = \dfrac{5}{4}.\)
Trục đối xứng là đường thẳng: \(x = \dfrac{5}{4}.\)
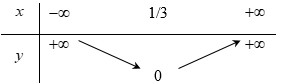
Đỉnh $I$ của parabol $(P): y = –3x^2+ 6x – 1$ là:
Ta có:
\(\begin{array}{l}\dfrac{{ - b}}{{2a}} = \dfrac{{ - 6}}{{2.( - 3)}} = \dfrac{{ - 6}}{{ - 6}} = 1\\\dfrac{{ - \Delta }}{{4a}} = \dfrac{{ - ({b^2} - 4ac)}}{{4a}} = \dfrac{{ - {6^2} + 4.( - 3).( - 1)}}{{4.( - 3)}} = \dfrac{{ - 36 + 12}}{{ - 12}} = \dfrac{{ - 24}}{{ - 12}} = 2.\end{array}\)
Suy ra đỉnh của Parabol là: $I(1;2)$
Biết parabol $(P): y = ax^2+ 2x + 5$ đi qua điểm $A(2; 1).$ Giá trị của $a$ là:
Parabol đi qua điểm $A(2; 1)$ nên ta có:\(4a + 4 + 5 = 1 \Leftrightarrow 4a = - 8 \Leftrightarrow a = - 2\)
Đỉnh của parabol $y = x^2+ x + m$ nằm trên đường thẳng $y = \dfrac{3}{4}$ nếu $m$ bằng:
Yêu cầu bài toán $ \Leftrightarrow \dfrac{{ - {b^2} + 4ac}}{{4a}} = \dfrac{3}{4} \Leftrightarrow \dfrac{{ - 1 + 4m}}{4} = \dfrac{3}{4} \Leftrightarrow 4m = 4 \Leftrightarrow m = 1$
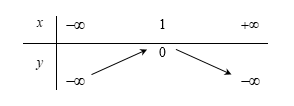
Bảng biến thiên của hàm số $y = –x^2+ 2x – 1$ là:
Ta có:
\(\begin{array}{l}a = - 1 < 0\,\,;\,\,\dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.( - 1)}} = \dfrac{{ - 2}}{{ - 2}} = 1\\y(1) = - {1^2} + 2.1 - 1 = 0.\end{array}\)
Suy ra bảng biến thiên:
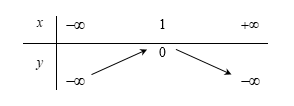
Cho hàm số $y = f(x) = ax^2 + bx +c.$ Rút gọn biểu thức $f(x + 3) – 3f(x + 2) + 3f(x + 1) $ ta được:
Ta có:
\(f(x+3)=a(x+3)^2+b(x+3)+c\\f(x+2)=a(x+2)^2+b(x+2)+c\\f(x+1)=a(x+1)^2+b(x+1)+c\)
$\Rightarrow f(x + 3) - 3f(x + 2) + 3f(x + 1)$ $= a{(x + 3)^2 } + b(x + 3) + c - 3a{(x + 2)^2} - 3b(x + 2) - 3c + 3a{(x + 1)^2} + 3b(x + 1) + 3c$ $= {x^2}(a - 3a + 3a) + x(6a + b - 12a - 3b + 6a + 3b) + (9a + 3b + c - 12a - 6b - 3c + 3a + 3b + 3c)$ $= a{x^2} + bx + c$
Tìm tọa độ giao điểm của hai parabol: \(y = \dfrac{1}{2}{x^2} - x\) và \(y = - 2{x^2} + x + \dfrac{1}{2}\) là:
Phương trình hoành độ giao điểm của hai parabol :
$\begin{array}{l}\dfrac{1}{2}{x^2} - x = - 2{x^2} + x + \dfrac{1}{2} \Leftrightarrow 5{x^2} - 4x - 1 = 0\\ \Leftrightarrow (x - 1)(5x + 1) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = \dfrac{{ - 1}}{5}}\end{array}} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = \dfrac{1}{2}{.1^2} - 1 = - \dfrac{1}{2}\end{array} \right.\\\left\{ \begin{array}{l}x = \dfrac{{ - 1}}{5}\\y = \dfrac{1}{2}.{\left( {\dfrac{{ - 1}}{5}} \right)^2} - \dfrac{{ - 1}}{5} = \dfrac{{11}}{{50}}\end{array} \right.\end{array} \right.\end{array}$
Tọa độ giao điểm $\left( {1;\dfrac{{ - 1}}{2}} \right);\left( {\dfrac{{ - 1}}{5};\dfrac{{11}}{{50}}} \right)$
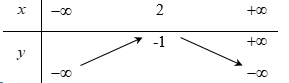
Cho hàm số \(y = - {x^2} + 2x + 1.\) Gọi $M$ và $m$ là giá trị lớn nhất vá giá trị nhỏ nhất của hàm số trên \(\left[ {0;2} \right]\). Tính giá trị của biểu thức \(T = {M^2} + {m^2}.\)
Hàm số \(y = - {x^2} + 2x + 1\) có \(a = - 1 < 0\,;\,\, - \dfrac{b}{{2a}} = 1 \Rightarrow \) Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
BBT:
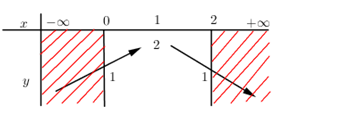
Dựa vào BBT ta thấy $M = 2$ và $m = 1$ \( \Rightarrow T = {M^2} + {m^2} = {2^2} + {1^2} = 5.\)
Hàm số nào sau đây có giá trị nhỏ nhất tại $x = \dfrac{3}{4}$?
Hàm số đạt GTNN nếu \(a > 0\) nên loại phương án B và C.
Phương án A: Hàm số có giá trị nhỏ nhất tại $x = - \dfrac{b}{{2a}} = \dfrac{3}{8}$ nên loại.
Còn lại chọn phương án D.
Cho hàm số \(y = f\left( x \right) = - {x^2} + 4x + 2\). Mệnh đề nào sau đây là đúng?
Ta có \(a = - 1 < 0\) nên hàm số $y$ tăng trên \(\left( { - \infty ;\,2} \right)\)và $y$ giảm trên \(\left( {2;\, + \infty } \right)\)nên chọn phương án A.
Hàm số nào sau đây nghịch biến trong khoảng \(\left( { - \infty ;\,0} \right)\)?
Đáp án A: \(a = \sqrt 2 > 0\) và \( - \dfrac{b}{{2a}} = 0\) nên hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\)
Đáp án B: \(a = - \sqrt 2 < 0\) và \( - \dfrac{b}{{2a}} = 0\) nên hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Đáp án C: \(y = \sqrt 2 \left( {{x^2} + 2x + 1} \right) = \sqrt 2 {x^2} + 2\sqrt 2 x + \sqrt 2 \) có \(a = \sqrt 2 > 0\) và \( - \dfrac{b}{{2a}} = - 1\) nên hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) nhưng \(\left( { - \infty ;0} \right) \not\subset \left( { - \infty ; - 1} \right)\) nên hàm số không nghịch biến trên \(\left( { - \infty ;0} \right)\)
Đáp án D: \(y = - \sqrt 2 \left( {{x^2} + 2x + 1} \right) = - \sqrt 2 {x^2} - 2\sqrt 2 x - \sqrt 2 \) có \(a = - \sqrt 2 < 0\) và \( - \dfrac{b}{{2a}} = - 1\) nên hàm số nghịch biến trên \(\left( { - 1; + \infty } \right)\)
Vậy chỉ có đáp án A đúng.
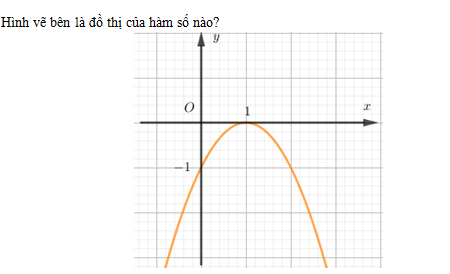
- Đồ thị hàm số đi qua điểm \(\left( {1;0} \right)\) nên loại A và C.
- Bề lõm hướng xuống dưới nên \(a < 0\).
Giao điểm của parabol \(\left( P \right)\): \(y = {x^2} + 5x + 4\) với trục hoành:
- Xét phương trình hoành độ giao điểm: \({x^2} + 5x + 4 = 0\).
- Phương trình có hai nghiệm \({x_1} = - 1;{x_2} = - 4\) nên các giao điểm là \(\left( { - 1;0} \right),\left( { - 4;0} \right)\).
Khi tịnh tiến parabol \(y = 2{x^2}\) sang trái $3$ đơn vị, ta được đồ thị của hàm số:
Tịnh tiến đồ thị hàm số \(y = 2{x^2}\) sang trái \(3\) đơn vị ta được đồ thị hàm số \(y = 2.{\left( {x + 3} \right)^2}\).
Tìm giá trị thực của tham số \(m \ne 0\) để hàm số \(y = m{x^2} - 2mx - 3m - 2\) có giá trị nhỏ nhất bằng \( - 10\) trên \(\mathbb{R}.\)
Ta có \(x = - \dfrac{b}{{2a}} = \dfrac{{2m}}{{2m}} = 1\), suy ra \(y = - 4m - 2\).
Hàm số có giá trị nhỏ nhất bằng \( - 10\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\ - 4m - 2 = - 10\end{array} \right. \Leftrightarrow m = 2\).
Nếu hàm số $y = a{x^2} + bx + c$ có $a < 0,b > 0$ và $c > 0$ thì đồ thị của nó có dạng:
+ \(a < 0\) nên loại đáp án A,B.
+ \(c > 0\) nên giao điểm của đồ thị với trục tung có tung độ dương, chọn đáp án D.
Ngoài ra các em cũng có thể nhận xét vì \(b > 0,a < 0\) nên hoành độ đỉnh \( - \dfrac{b}{{2a}} > 0\) và đáp án D thỏa mãn.
Cho parabol $\left( P \right):{\rm{ }}y = - 3{x^2} + 6x-1$. Khẳng định đúng nhất trong các khẳng định sau là:
- Ta có \(a = - 3 < 0\) và \(x = - \dfrac{b}{{2a}} = 1 \Rightarrow I(1,2)\)
- Đường thẳng \(x = 1\) là trục đối xứng.
- Đồ thị hàm số cắt trục \(Oy\) \( \Rightarrow x = 0 \Rightarrow y = - 1\) .
Cho parabol $\left( P \right):y = a{x^2} + bx + 2$ biết rằng parabol đó cắt trục hoành tại hai điểm lần lượt có hoành độ ${x_1} = 1$ và ${x_2} = 2$. Parabol đó là:
- Parabol $\left( P \right)$cắt $Ox$ tại $A\left( {1;0} \right),{\rm{ }}B\left( {2;0} \right)$.
- Khi đó $\left\{ \begin{array}{l}A \in \left( P \right)\\B \in \left( P \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a + b + 2 = 0\\4a + 2b + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b = - 2\\2a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 3\end{array} \right.$
Vậy $\left( P \right):y = {x^2} - 3x + 2$.
Cho hàm số \(y = a{x^2} + bx + c\left( {a < 0} \right)\) có đồ thị \(\left( P \right)\). Khẳng định nào sau đây là khẳng định đúng?
Hàm số \(y = a{x^2} + bx + c\left( {a < 0} \right)\) đồng biến trên khoảng \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và nghịch biến trên khoảng \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)
Nên A, B sai.
Ta chưa kết luận được gì về số giao điểm của đồ thị hàm số đã cho với trục hoành nên C sai.
Đồ thị hàm số \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) có trục đối xứng là đường thẳng \(x = - \dfrac{b}{{2a}}\) nên D đúng.
Cho hàm số \(\left( P \right):\,\,y = {x^2} + 4x - 2\). Điểm nào dưới đây thuộc đồ thị hàm số \(\left( P \right)\)?
Đáp án A: \({1^2} + 4.1 - 2 = 3 \ne - 3 \Rightarrow \left( {1; - 3} \right)\) không thuộc \(\left( P \right)\).
Đáp án B: \({3^2} + 4.3 - 2 = 19 \ne 18 \Rightarrow \left( {3;18} \right)\) không thuộc \(\left( P \right)\).
Đáp án C: \({\left( { - 2} \right)^2} + 4.\left( { - 2} \right) - 2 = - 6 \Rightarrow \left( { - 2; - 6} \right)\) thuộc \(\left( P \right)\).