Câu hỏi:
3 năm trước
Cho hàm số \(y = - {x^2} + 2x + 1.\) Gọi $M$ và $m$ là giá trị lớn nhất vá giá trị nhỏ nhất của hàm số trên \(\left[ {0;2} \right]\). Tính giá trị của biểu thức \(T = {M^2} + {m^2}.\)
Trả lời bởi giáo viên
Đáp án đúng: a
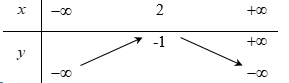
Hàm số \(y = - {x^2} + 2x + 1\) có \(a = - 1 < 0\,;\,\, - \dfrac{b}{{2a}} = 1 \Rightarrow \) Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
BBT:
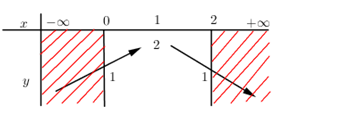
Dựa vào BBT ta thấy $M = 2$ và $m = 1$ \( \Rightarrow T = {M^2} + {m^2} = {2^2} + {1^2} = 5.\)
Hướng dẫn giải:
Lập BBT của hàm số trên một đoạn để tìm GTLN và GTNN của hàm số trên đoạn đó.