Hàm số bậc hai

Hàm số $y = a{x^2} + bx + c,\,\,a \ne 0$ là hàm số bậc 2 nên có đỉnh $I\left( {\dfrac{{ - b}}{{2a}};\dfrac{{ - \Delta }}{{4a}}} \right)$

Vì hàm số đạt giá trị lớn nhất trên $\mathbb{R}$ bằng 4 khi $x =  - 1$ nên đồ thị hàm số có đỉnh $I\left( { - 1;4} \right)$ và $a < 0.$

$\Rightarrow \left\{ \begin{array}{l}\dfrac{{ - b}}{{2a}} =  - 1\\f\left( { - 1} \right) = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\a - b + c = 4\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}b = 2a\\a - 2a + c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\c = 4 + a\end{array} \right.$

Xét phương trình: $y = 0$ $\Leftrightarrow a{x^2} + bx + c = 0$ có hai nghiệm ${x_1};\,\,{x_2}$ $\Leftrightarrow \Delta  > 0 \Leftrightarrow {b^2} - 4ac > 0.$

Áp dụng định lý Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..$

Theo đề bài ta có: $x_1^2 + x_2^2 = 10 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10$

$\begin{array}{l} \Leftrightarrow {\left( { - \dfrac{b}{a}} \right)^2} - \dfrac{{2c}}{a} = 10\\ \Leftrightarrow {\left( { - \dfrac{{2a}}{a}} \right)^2} - \dfrac{{2c}}{a} = 10\\ \Leftrightarrow 4a - 2c = 10a\\ \Leftrightarrow 6a + 2c = 0\\ \Leftrightarrow 6a + 2\left( {4 + a} \right) = 0\\ \Leftrightarrow 6a + 2a + 8 = 0\\ \Leftrightarrow a =  - 1\,\,\left( {tm} \right)\\ \Rightarrow \left\{ \begin{array}{l}b =  - 2\\c = 3\end{array} \right..\\ \Rightarrow y =  - {x^2} - 2x + 3.\end{array}$

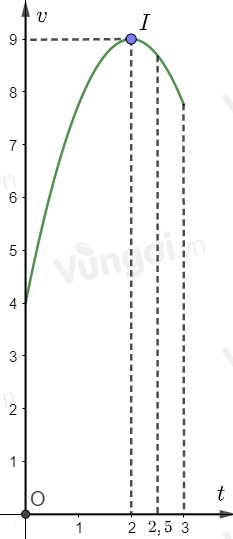
Vì vận tốc $v\,\,\left( {km/h} \right)$ phụ thuộc thời gian $t\,\,\left( h \right)$ có đồ thị là một phần của parabol nên ta có hàm số $v =f(t)= a{t^2} + bt + c\,\,\,\left( {a \ne 0} \right)$.

Dựa vào đồ thị hàm số ta có: tại thời điểm $t = 0$, $v = 4$$\Rightarrow a.0^2+b.0+c=4 \Rightarrow c = 4$

Đồ thị hàm số có đỉnh $I\left( {2;9} \right)$$\Rightarrow \left\{ \begin{array}{l}\dfrac{{ - b}}{{2a}} = 2\\f\left( 2 \right) = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 4a\\a{.2^2} + b.2 + 4 = 9\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b = 5\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{ - 5}}{4}\\b = 5\end{array} \right.$

$\Rightarrow v =  - \dfrac{5}{4}{t^2} + 5t + 4$

Tại lúc 2 giờ 30 phút = 2,5 giờ vận tốc đạt được là:

$v\left( {2,5} \right) = \dfrac{{ - 5}}{4}.2,{5^2} + 5.2,5 + 4$$= 8,6875\,\,\left( {km/h} \right) \approx 8,7\,\,\left( {km/h} \right)$

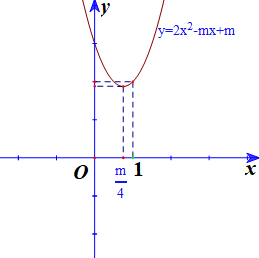
Hàm số $y = 2{x^2} - mx + m$ đồng biến trên $\left( {\dfrac{m}{4}; + \infty } \right)$ nên để hàm số đồng biến trên $\left( {1; + \infty } \right)$ thì $\left( {1; + \infty } \right) \subset \left( {\dfrac{m}{4}; + \infty } \right)$

$\Rightarrow \dfrac{m}{4} \le 1 \Leftrightarrow m \le 4$.

Vậy $m \in \left( { - \infty ;4} \right]$.

Ta có $h\left( t \right) = 3 + 10t - 2{t^2}$ có đồ thị là parabol có bề lõm hướng xuống, đạt GTLN tại $t = \dfrac{{ - 10}}{{2.\left( { - 2} \right)}} = \dfrac{5}{2}$.

Vậy $\max h\left( t \right) = h\left( {\dfrac{5}{2}} \right) = \dfrac{{31}}{2}\,\,\left( m \right)$.

Parabol $y = a{x^2} + bx + c$ đạt cực đại bằng $4$ khi $x =  - 2 \Rightarrow$ parabol  có đỉnh  $I\left( { - 2;4} \right)$

Lại có parabol đi qua điểm $A\left( {0;6} \right)$ nên ta có:  $\left\{ {\begin{array}{*{20}{c}}{4a - 2b + c = 4}\\\begin{array}{l}c = 6\\ - \dfrac{b}{{2a}} =  - 2\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \dfrac{1}{2}}\\{b = 2}\\{c = 6}\end{array}} \right.} \right.$ .

Vậy parabol đã cho có hàm số: $y = \dfrac{1}{2}{x^2} + 2x + 6.$

Đồ thị hàm số $y =  - {x^2} + 4x - 1$ có đỉnh $I\left( {2;3} \right)$ và có hệ số $a < 0\,\,\, \Rightarrow$ Hàm số đạt GTLN bằng 3 khi $x = 2$.

Bước 1: Xác định hệ số $a$

Ta có $a=-1<0$

Hàm số đã cho đạt giá trị lớn nhất tại $x =  - {b \over {2a}} =  1$.

Bước 2: Tìm giá trị của hàm số tại $x=-\dfrac{b}{2a}$, tìm $m$.

Khi đó $Maxy = f\left( 1 \right) = m - 4$.

Để $Maxy = 6$ thì $m - 4 = 6 \Leftrightarrow m = 10$.

Bước 1:

Xét hàm số $y = {x^2} - 2x + 5$ trên $\left[ {2;\,\,7} \right]$ ta có BBT:

Đỉnh của đồ thị hàm số $y = {x^2} - 2x + 5$ là $I\left( {1;\,\,4} \right)$

Ta thấy $1 \notin [2;7]$. Ta lập bảng biến thiên:

Bước 2:

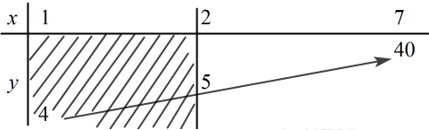
Dựa vào BBT ta có: $M = \mathop {Max}\limits_{\left[ {2;\,\,7} \right]} y = 40$ khi $x = 7$ và $m = \mathop {Min}\limits_{\left[ {2;\,\,7} \right]} y = 5$ khi $x = 2.$

$\Rightarrow M = 8m$