Bài toán về hàm phân thức có tham số
Kỳ thi ĐGNL ĐHQG Hà Nội
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:
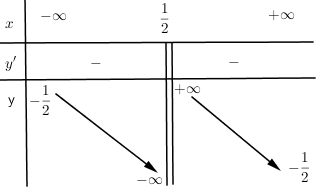
Khẳng định nào sau đây là đúng?
$x = \dfrac{1}{2}$ là tiệm cận đứng của đồ thị hàm số
$y = - \dfrac{1}{2}$ là tiệm cận ngang của đồ thị hàm số
Hàm số nghịch biến trên $\left( { - \infty ;\,\dfrac{1}{2}} \right)$ và $\left( {\dfrac{1}{2};\, + \infty } \right)$
Cho hàm số $y = f\left( x \right)$có bảng biến thiên:
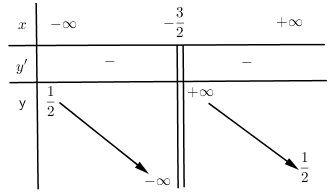
Khẳng định nào sau đây là đúng?
Nhận xét:
$x = - \dfrac{3}{2}$ là tiệm cận đứng của đồ thị hàm số
$y = \dfrac{1}{2}$ là tiệm cận ngang của đồ thị hàm số
Hàm số nghịch biến trên $\left( { - \infty ;\, - \dfrac{3}{2}} \right)$ và $\left( { - \dfrac{3}{2};\, + \infty } \right)$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:
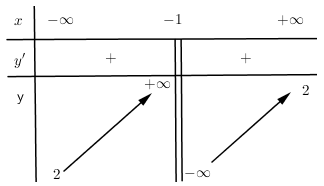
Khẳng định nào sau đây là sai?
Nhận xét:
$x = - 1$ là tiệm cận đứng của đồ thị hàm số
$y = 2$ là tiệm cận ngang của đồ thị hàm số
Hàm số đồng biến trên $\left( { - \infty ; - 1} \right)$ và $\left( { - 1;\, + \infty } \right)$
Þ Khẳng định sai là: Đồ thị hàm số có tiệm cận ngang là $y = - 1$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên
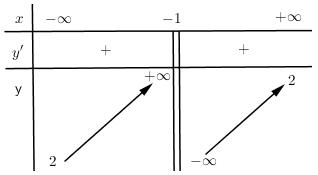
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là:
Từ bảng biến thiên ta có:
- Tiệm cận đứng của đồ thị hàm số là $x = - 1.$
- Tiệm cận ngang của đồ thị hàm số là $y = 2.$
Vậy tiệm cận đứng và tiệm cận ngang của đồ thị hàm số cắt nhau tại điểm có tọa độ là $\left( { - 1;2} \right)$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
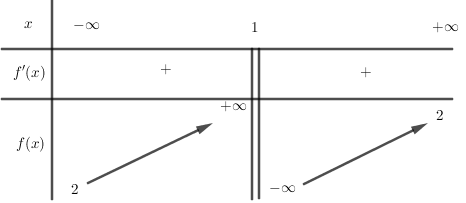
A đúng vì đồ thị hàm số có đường tiệm cận đứng là \(x = 1\)
B đúng vì hàm số luôn đồng biến nên không có cực trị
C đúng vì đồ thị hàm số có đường tiệm cận ngang \(y = 2\)
D sai vì hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) chứ không đồng biến trên toàn bộ tập số thực \(\mathbb{R}\)
Cho hàm số $y = \dfrac{5}{{x - 2}}$ . Khẳng định nào sau đây là đúng?
Ta có: $y' = - \dfrac{5}{{{{\left( {x - 2} \right)}^2}}} < 0$ $\forall x \in D$
Hàm số nghịch biến trên khoảng $\left( { - \infty ;2} \right)$ và $\left( {2; + \infty } \right)$
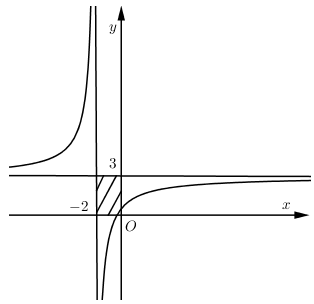
Giao điểm của hai đường tiệm cận của đồ thị hàm số nào dưới đây nằm trên đường thẳng $d:y = x$?
Đáp án A có giao hai đường tiệm cận là $\left( { - 3;2} \right) \notin d$
Đáp án B có giao hai đường tiệm cận là $\left( {1;1} \right) \in d$
Đáp án C có giao hai đường tiệm cận là $\left( { - 2;2} \right) \notin d$
Đáp án D có giao hai đường tiệm cận là $\left( { - 3;0} \right) \notin d$
Cho hàm số $y = \dfrac{{x + 2}}{{x - 3}}$ có đồ thị $\left( C \right)$. Có bao nhiêu tiêu điểm $M$ thuộc $\left( C \right)$ sao cho khoảng cách từ điểm $M$ đến tiệm cận ngang bằng $5$ lần khoảng cách từ điểm $M$ đến tiệm cận đứng.
Đồ thị hàm số có đường tiệm cận ngang là $y = 1 \Leftrightarrow y-1=0$
Đồ thị hàm số có đường tiệm cận đứng là $x = 3\Leftrightarrow x-3=0$
Giả sử $M\left( {{x_0};\dfrac{{{x_0} + 2}}{{{x_0} - 3}}} \right)$ thuộc đồ thị hàm số.
Từ đề bài ta có phương trình
$5\left| {{x_0} - 3} \right| = \left| {\dfrac{{{x_0} + 2}}{{{x_0} - 3}} - 1} \right| \Leftrightarrow 5\left| {{x_0} - 3} \right| = \left| {\dfrac{5}{{{x_0} - 3}}} \right| \Leftrightarrow {\left( {{x_0} - 3} \right)^2} = 1 $
$\Leftrightarrow \left[ \begin{gathered} x - 3 = - 1 \hfill \\ x - 3 = 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} {x_0} = 2 \hfill \\ {x_0} = 4 \hfill \\ \end{gathered} \right.$
Vậy ta có hai điểm thỏa mãn đề bài là $\left( {2; - 4} \right)$ và $\left( {4;6} \right)$
Cho hàm số $y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).$ Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
Đồ thị hàm số $y = \dfrac{{3x + 1}}{{x + 2}}$ có:
- Tiệm cận đứng là $x = - 2$.
- Tiệm cận ngang là $y = 3$.
Diện tích hình chữ nhật được tạo bởi 2 tiệm cận là: $S=\left| -2 \right|.\left| 3 \right|=6$ đvdt
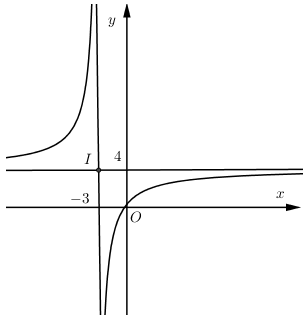
Cho hàm số $y = \dfrac{{4x + 1}}{{x + 3}}\left( C \right).$ Khoảng cách từ giao điểm 2 đường tiệm cận của (C) đến gốc tọa độ bằng:
Đồ thị hàm số $y = \dfrac{{4x + 1}}{{x + 3}}$ có:
- Tiệm cận đứng $x = - 3$.
- Tiệm cận ngang $y = 4$.
- Giao 2 tiệm cận: $I\left( { - 3;\,4} \right)$
$\overrightarrow {OI} \left( { - 3;4} \right) \to OI = \sqrt {{{\left( { - 3} \right)}^2} + {4^2}} = 5$
Þ Khoảng cách từ giao điểm 2 đường tiệm cận của (C) đến gốc tọa độ bằng $5$
Cho hàm số $y = \dfrac{{ax - 1}}{{x + d}}$ có bảng biến thiên
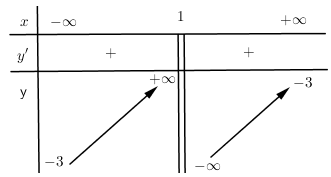
Giá trị của ${a^2} + {d^2}$ bằng:
Xét hàm số $y = \dfrac{{ax - 1}}{{x + d}}$
+) Tiệm cận đứng $x = - d$ mà theo bảng biến thiên tiệm cận đứng của đồ thị hàm số là \(x = 1\) suy ra $d = - 1$.
+) Tiệm cận ngang $y = \dfrac{a}{1}$ mà theo bảng biến thiên tiệm cận ngang của đồ thị hàm số là $y = - 3$ suy ra $a = - 3$.
Vậy: ${a^2} + {d^2} = {\left( { - 3} \right)^2} + {\left( { - 1} \right)^2} = 10$
Tìm giá trị của tham số \(m\) để đồ thị hàm số \(y = \dfrac{{mx + 5}}{{x + 1}}\) đi qua \(A\left( {1; - 3} \right)\)
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Hàm số \(y = f\left( x \right) = \dfrac{{mx + 5}}{{x + 1}}\) đi qua \(A\left( {1; - 3} \right)\) nên ta có : \(f\left( 1 \right) = - 3 \Leftrightarrow \dfrac{{m + 5}}{{1 + 1}} = - 3 \Rightarrow m = - 11\)
Vậy \(m = - 11\) thì hàm số đã cho đi qua \(A\left( {1; - 3} \right)\).
Cho hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có bảng biến thiên:
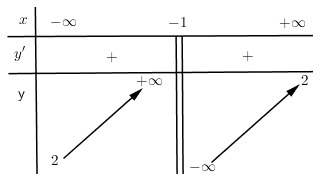
Giá trị của ${c^2} - {d^2}$ bằng:
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có $\left\{ \begin{gathered} \xrightarrow{{TCD}}x = - \dfrac{d}{c} = - 1 \hfill \\ \xrightarrow{{TCN}}y = \dfrac{2}{c} = 2 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} c = 1 \hfill \\ d = 1 \hfill \\ \end{gathered} \right. \Rightarrow {c^2} - {d^2} = {1^2} - {1^2} = 0$
Đồ thị hàm số $y = \dfrac{{ax + 2}}{{2x + d}}$ như hình vẽ bên.
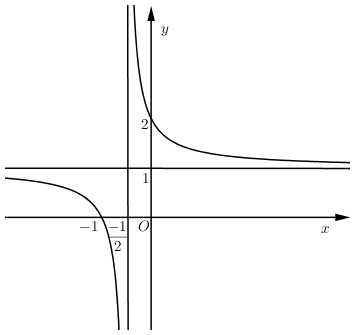
Chọn khẳng định đúng:
Đồ thị hàm số $y = \dfrac{{ax + 2}}{{2x + d}}$ có $\left\{ \begin{align} & \xrightarrow{TCD}x=-\dfrac{d}{2}=-\dfrac{1}{2}\Rightarrow d=1 \\ & \xrightarrow{TCN}y=\dfrac{a}{2}=1\Rightarrow a=2 \\ \end{align} \right.\Rightarrow 3a+d=7$
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
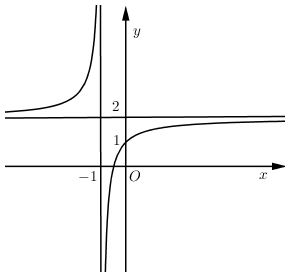
Chọn khẳng định đúng:
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có $\left\{ \begin{align}& \xrightarrow{TCN}y=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCD}x=-\dfrac{d}{c}=-\dfrac{d}{1}=-1\Rightarrow d=1 \\ \end{align} \right.$
Hàm số có dạng $y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)$
Ta có điểm $\left( {0;1} \right) \in \left( C \right)$
Thay $x = 0$ và $y = 1$ vào hàm số ta được $1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1$ $ \Rightarrow b + c + d = 3$
Đồ thị hàm số $y = \dfrac{{ax - b}}{{x - 1}}$ như hình vẽ bên
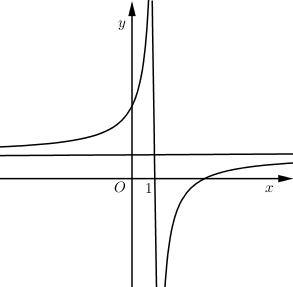
Chọn khẳng định đúng:
+) $y = \dfrac{{ax - b}}{{x - 1}} \Rightarrow y' = \dfrac{{ - a + b}}{{{{\left( {x - 1} \right)}^2}}}, \forall x\ne 1$
Hàm số đồng biến $ \Rightarrow y' > 0 \Leftrightarrow - a + b > 0 \Leftrightarrow b > a$
+) Tiệm cận ngang $y = \dfrac{a}{1} > 0 \Rightarrow a > 0$
Vậy $0 < a < b$
Đồ thị hàm số $y = \dfrac{{ax + 2}}{{cx + b}}$ như hình vẽ bên.
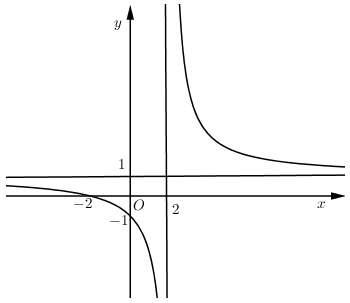
Chọn khẳng định đúng:
Ta có đồ thị hàm số$y = \dfrac{{ax + 2}}{{cx + b}}$ đi qua điểm có tọa độ $\left( {0; - 1} \right)$
Thay $x = 0;\,y = - 1$ vào hàm số ta được $ - 1 = \dfrac{{a.0 + 2}}{{c.0 + b}} \Rightarrow b = - 2$
Đồ thị hàm số $y = \dfrac{{ax + 2}}{{cx - 2}}$ có
$\left\{ \begin{align} & \xrightarrow{TCD}x=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCN}y=\dfrac{a}{c}=\dfrac{a}{1}=1\Rightarrow a=1 \\ \end{align} \right.$ $\Rightarrow a=1;\,b=-2;\,c=1$
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ như hình vẽ bên
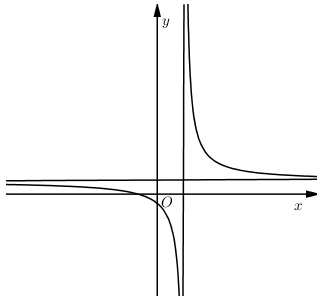
Chọn khẳng định đúng
+) Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ có:
- TCĐ: $x = - \dfrac{d}{c} > 0 \Rightarrow cd < 0 \Rightarrow $ Loại C.
- TCN: $y = \dfrac{a}{c} > 0 \Rightarrow ac > 0$
- Giao $Oy:x = 0$ $ \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow bd < 0 \Rightarrow $ Loại B.
- Giao $Ox:y = 0$ $ \Rightarrow x = - \dfrac{b}{a} < 0 \Rightarrow ab > 0$
Vì $ac > 0;ab > 0$ nên $ab.ac > 0 \Rightarrow bc > 0$
Vì $ab > 0;bd < 0$ nên $ab.bd < 0 \Rightarrow ad < 0 \Rightarrow $Loại D.
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ như hình vẽ bên
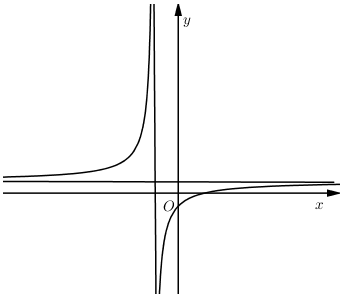
Chọn khẳng định đúng
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ có:
- TCĐ $x = - \dfrac{d}{c} < 0 \Rightarrow cd > 0$
- TCN $y = \dfrac{a}{c} > 0 \Rightarrow ac > 0$
$ \Rightarrow ac.cd > 0 \Rightarrow ad > 0 \Rightarrow $Loại A, B.
- $y' = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}} > 0 \Rightarrow ad > bc$
- Cắt $Oy:x = 0 \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow bd < 0$
- Cắt $Ox:y = 0 \Rightarrow x = - \dfrac{b}{a} > 0 \Rightarrow ab < 0$
Vì $ac > 0;ab < 0$ nên $ac.ab < 0 \Rightarrow bc < 0 \Rightarrow $ Loại D
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ như hình vẽ bên
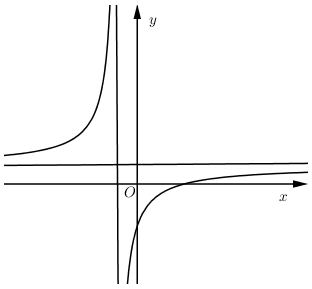
Chọn khẳng định đúng
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ có:
- TCĐ: $x = - \dfrac{d}{c} < 0 \Rightarrow cd > 0$.
- TCN: $y = \dfrac{a}{c} > 0 \Rightarrow ac > 0$.
$ \Rightarrow cd.ac > 0 \Rightarrow ad > 0 \Rightarrow $ Loại D.
- Giao $Oy:x = 0 \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow bd < 0 \Rightarrow $Loại C.
- Giao $Ox:y = 0 \Rightarrow x = - \dfrac{b}{a} > 0 \Rightarrow ab < 0 \Rightarrow $Loại A.

