Câu hỏi:
2 năm trước
Cho hàm số y=4x+1x+3(C). Khoảng cách từ giao điểm 2 đường tiệm cận của (C) đến gốc tọa độ bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
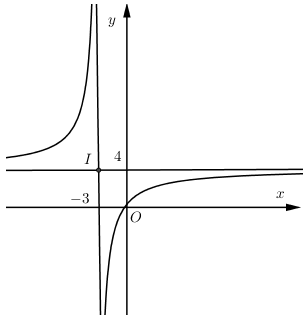
Đồ thị hàm số y=4x+1x+3 có:
- Tiệm cận đứng x=−3.
- Tiệm cận ngang y=4.
- Giao 2 tiệm cận: I(−3;4)
→OI(−3;4)→OI=√(−3)2+42=5
Þ Khoảng cách từ giao điểm 2 đường tiệm cận của (C) đến gốc tọa độ bằng 5
Hướng dẫn giải:
- Tìm các đường tiệm cận của đồ thị hàm số.
- Tìm giao điểm hai đường tiệm cận và tính khoảng cách.