Câu hỏi:
2 năm trước
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ như hình vẽ bên
Chọn khẳng định đúng
Trả lời bởi giáo viên
Đáp án đúng: a
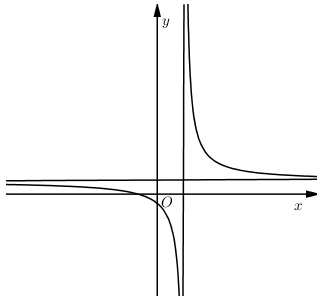
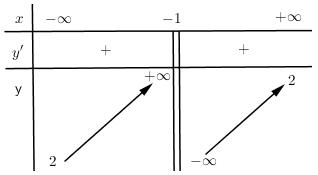
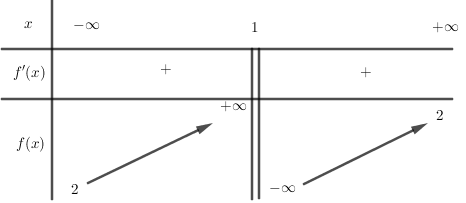
+) Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ có:
- TCĐ: $x = - \dfrac{d}{c} > 0 \Rightarrow cd < 0 \Rightarrow $ Loại C.
- TCN: $y = \dfrac{a}{c} > 0 \Rightarrow ac > 0$
- Giao $Oy:x = 0$ $ \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow bd < 0 \Rightarrow $ Loại B.
- Giao $Ox:y = 0$ $ \Rightarrow x = - \dfrac{b}{a} < 0 \Rightarrow ab > 0$
Vì $ac > 0;ab > 0$ nên $ab.ac > 0 \Rightarrow bc > 0$
Vì $ab > 0;bd < 0$ nên $ab.bd < 0 \Rightarrow ad < 0 \Rightarrow $Loại D.
Hướng dẫn giải:
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số.
- Tìm các giao điểm của đồ thị hàm số với các trục tọa độ.
- Xét tính đơn điệu của hàm số.
- Kết hợp các điều trên để tìm điều kiện của $a,b,c,d$.
Câu hỏi khác
- Bài tập phần cực trị của hàm số thi ĐGNL ĐHQG HN
- Bài tập phần bài toán liên quan đến khảo sát hàm số bậc ba, bậc bốn trùng phương có tham số thi ĐGNL ĐHQG HN
- Bài tập phần bài toán cực trị có tham số đối với một số hàm số cơ bản thi ĐGNL ĐHQG HN
- Bài tập phần giá trị lớn nhất, nhỏ nhất của hàm số thi ĐGNL HN
- Bài tập sự đồng biến, nghịch biến thi ĐGNL HN
