Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
Công thức tính thể tích khối chóp V=13Sh.
Phép vị tự tỉ số k>0 biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó:
Phép vị tự tỉ số k>0 biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó V′V=k3.
Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:
Nếu A′,B′,C′ là ba điểm lần lượt nằm trên các cạnh SA,SB,SC của hình chóp tam giác S.ABC. Khi đó:
VS.A′B′C′VS.ABC=SA′SA.SB′SB.SC′SC
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
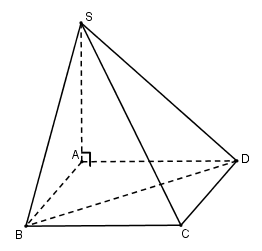
Ta có: SΔBCD=12SABCD=12a2
VS.BCD=13SA.SBCD=13a.12a2=a36
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn SA⊥(ABCD) và AB=2AD=2CD=2a=√2SA. Thể tích khối chóp S.BCD là:
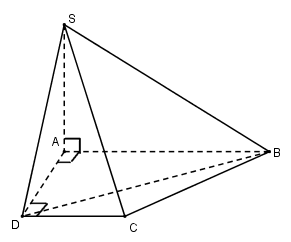
Ta có: SABCD=12(AB+CD).AD=12(2a+a)a=3a22
SΔABD=12AD.AB=12a.2a=a2
⇒SBCD=SABCD−SABD=3a22−a2=a22
SA=2a√2=a√2
⇒VS.BCD=13SA.SBCD=13a√2.a22=a3√26
Cho hình chóp S.ABCD có SA⊥(ABCD). Biết AC=a√2, cạnh SC tạo với đáy một góc 600 và diện tích tứ giác ABCD là 3a22. Gọi H là hình chiếu của A trên cạnh SC. Tính thể tích khối chóp H.ABCD.
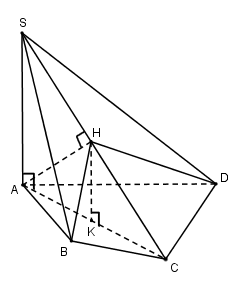
Ta có: SA⊥(ABCD)⇒AClà hình chiếu của SC trên (ABCD)⇒^(SC;(ABCD))=^(SC;AC)=600
SA⊥(ABCD)⇒SA⊥AC⇒ΔSAC vuông tại A và ^SCA=600
Xét tam giác vuông SAC có: SA=AC.tan60=a√2.√3=a√6;SC=ACcos60=a√212=2a√2
Áp dụng hệ thức lượng trong tam giác vuông SAC có: AC2=HC.SC⇒HCSC=AC2SC2=2a28a2=14
Trong (SAC) kẻ HK//SA⇒HK⊥(ABCD)
Ta có: HKSA=HCSC=14⇒HK=14SA=a√64
Vậy VH.ABCD=13HK.SABCD=13.a√64.3a22=a3√68
Cho hình chóp S.ABC có SA⊥SB,SB⊥SC,SA⊥SC;SA=2a,SB=b,SC=c. Thể tích khối chóp là:
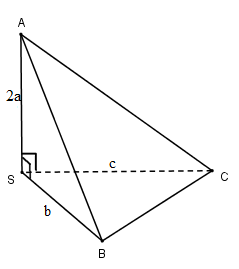
Ta có: SA⊥SBSA⊥SCSB⊥SC}⇒S.ABC là tứ diện vuông.
⇒VS.ABC=16SA.SB.SC=16.2a.b.c=13abc.
Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết SB=a,SC hợp với (SAB) một góc 300 và (SAC) hợp với đáy (ABC) một góc 600. Thể tích khối chóp là:
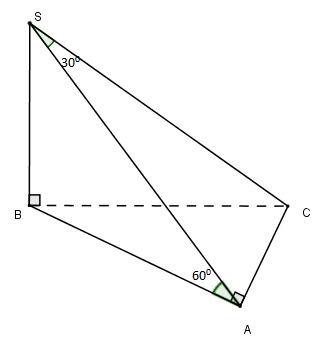
Ta có:
AC⊥ABAC⊥SB(SB⊥(ABC))}⇒AC⊥(SAB)⇒AC⊥SA
⇒SA là hình chiếu vuông góc của SC trên (SAB)⇒^(SC;(SAB))=^(SC;SA)=^CSA=300
(SAC)∩(ABC)=AC(SAC)⊃SA⊥AC(ABC)⊃AB⊥AC}⇒^((SAC);(ABC))=^(SA;AB)=^SAB=600
SB⊥(ABC)⇒SB⊥AB⇒ΔSAB vuông tại B
⇒AB=SB.cot600=a.1√3=a√33
⇒SA=√SB2+AB2=√a2+a23=2a√3
Xét tam giác vuông SAC ta có: AC=SA.tan300=2a√3.1√3=2a3
SABC=12AB.AC=12a√33.2a3=a2√39
VS.ABC=13SB.SABC=13.a.a2√39=a3√327
Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau, AB=6a,AC=7a,AD=4a. Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CD,DB. Thể tích V của tứ diện AMNP là:
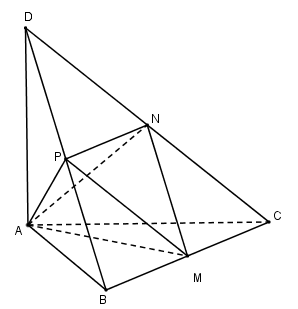
Ta có:
ABCD là tứ diện vuông tại A nên VABCD=16AB.AC.AD=16.6a.7a.4a=28a3.
Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện ta có:
VDAPNVDABC=DADA.DPDB.DNDC=11.12.12=14⇒VDAPN=14VDABC=14.28a3=7a3
VBAPMVBADC=BABA.BPBD.BMBC=11.12.12=14⇒VBAPM=14VBADC=14.28a3=7a3
VCAMNVCABD=CACA.CMCB.CNCD=11.12.12=14⇒VCAMN=14VCABD=14.28a3=7a3
Do đó VAMNP=VABCD−VDAPN−VBAPM−VCAMN=28a3−7a3−7a3−7a3=7a3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc 450. Gọi M,N lần lượt là trung điểm của AB và AD. Thể tích của khối chóp S.MCDN là:
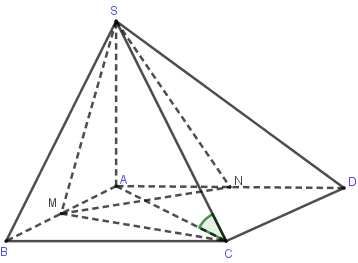
(SAB)⊥(ABCD)(SAD)⊥(ABCD)(SAB)∩(SAD)=SA}⇒SA⊥(ABCD)
⇒AC là hình chiếu vuông góc của SC trên (ABCD)⇒^(SC;(ABCD))=^(SC;AC)=^SCA=450
(vì SA⊥(ABCD)⇒SA⊥AC⇒ΔSAC vuông tại A⇒^SCA<90o)
⇒SA=AC=a√2
SABCD=a2SAMN=12AM.AN=12a2a2=a28SBCM=12BM.BC=12a2.a=a24⇒SMCDN=SABCD−SAMN−SBCM=a2−a28−a24=5a28⇒VS.MCDN=13SA.SMCDN=13a√2.5a28=5a3√224
Cho khối lăng trụ tam giác đều ABC.A1B1C1 có tất cả các cạnh bằng a. Gọi M là trung điểm của AA1. Thể tích khối chóp M.BCA1 là:
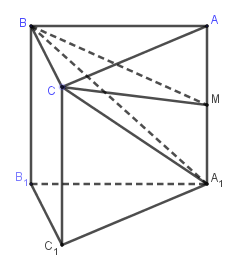
ΔABC là tam giác đều cạnh a nên có diện tích SABC=a2√34
Ta có AM=AA12=a2
Hai tứ diện MABC và MA1BC có chung đỉnh C, diện tích hai đáy MAB và MA1B bằng nhau nên có thể tích bằng nhau, suy ra
VM.BCA1=VM.ABC=13AM.SABC=a3√324
Cho hình chóp đều S.ABCD có cạnh bên và cạnh đáy bằng a. Thể tích của khối chóp S.ABCD là:
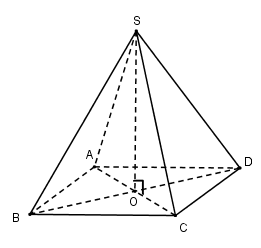
Gọi O=AC∩BD
Vì chóp S.ABCD đều nên SO⊥(ABCD)
Ta có: AC=BD=a√2⇒OA=12AC=a√22
SO⊥(ABCD)⇒SO⊥OA⇒ΔSOA vuông tại O ⇒SO=√SA2−OA2=√a2−a22=a√22
Vậy VS.ABCD=13SO.SABCD=13a√22a2=a3√26
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600. Tính thể tích khối chóp S.ABC?
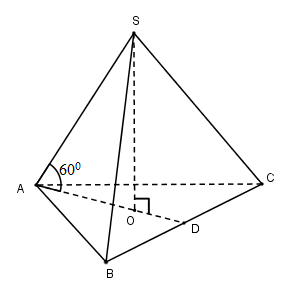
Gọi O là trọng tâm tam giác đều ABC
Vì chóp S.ABC đều nên SO⊥(ABC)
⇒OA là hình chiếu vuông góc của SA lên (ABC)⇒^(SA;(ABC))=^(SA;OA)=^SAO=600
SO⊥(ABC)⇒SO⊥OA⇒ΔSAO vuông tại O
Gọi D là trung điểm của BC ta có: AD=a√32⇒AO=23AD=23a√32=a√33
⇒SO=AO.tan60=a√33.√3=a
Vì tam giác ABC đều nên SΔABC=a2√34
Vậy VS.ABC=13SO.SΔABC=13aa2√34=a3√312
Cho hình chóp đều S.ABCD có diện tích đáy là 16cm2, diện tích một mặt bên là 8√3cm2. Thể tích khối chóp S.ABCD là:
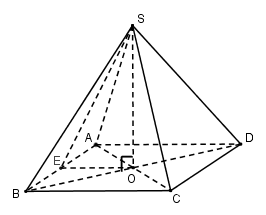
Gọi O=AC∩BD. Vì chóp S.ABCD đều nên SO⊥(ABCD)
Vì chóp S.ABCD đều nên ABCD là hình vuông ⇒SABCD=AB2=16⇒AB=4(cm)=AD
Gọi E là trung điểm của AB⇒OE là đường trung bình của tam giác ABD⇒OE//AD⇒OE⊥AB và OE=12AD=12.4=2(cm)
OE⊥ABSO⊥AB(SO⊥(ABCD))}⇒AB⊥(SOE)⇒AB⊥SE
⇒SΔSAB=12SE.AB=8√3⇒SE=16√3AB=16√34=4√3(cm)
SO⊥(ABCD)⇒SO⊥OE⇒ΔSOE vuông tại O⇒SO=√SE2−OE2=√48−4=√44=2√11(cm)
Vậy VS.ABCD=13SO.SABCD=13.2√11.16=32√113(cm3)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 600. Thể tích khối chóp S.ABC là:
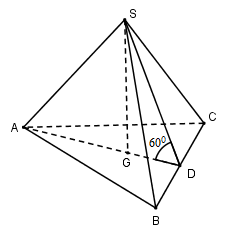
Bước 1:
Gọi G là trọng tâm tam giác ABC. Vì chóp S.ABC đều nên SG⊥(ABC)
Gọi D là trung điểm của BC ta có: AD⊥BC
Ta có: BC⊥ADBC⊥SG(SG⊥(ABC))}⇒BC⊥(SAD)⇒BC⊥SD
(SBC)∩(ABC)=BC(SBC)⊃SD⊥BC(ABC)⊃AD⊥BC}⇒^((SBC);(ABC))=^(SD;AD)=^SDA=600
Bước 2:
Vì tam giác ABC đều cạnh a nên AD=a√32⇒DG=13AD=a√36
SG⊥(ABC)⇒SG⊥AD⇒ΔSGD vuông tại G
⇒SG=GD.tan60=a√36.√3=a2
Bước 3:
Tam giác ABC đều ⇒SΔABC=a2√34
Bước 4:
⇒VS.ABC=13SG.SΔABC=13.a2.a2√34=a3√324
Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 600. Thể tích hình chóp là:
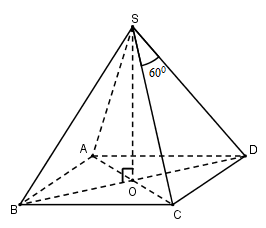
Gọi O=AC∩BD.
Vì chóp S.ABCD đều nên SO⊥(ABCD)
Đặt SA=SB=SC=SD=a
Tam giác SCD có:SC=SD;^CSD=600⇒ΔSCD đều⇒CD=SC=SD=a
⇒ Hình vuông ABCD cạnh a⇒AC=BD=a√2⇒OC=12AC=a√22
SO⊥(ABCD)⇒SO⊥OC⇒ΔSOC vuông tại O
⇒SO=√SC2−OC2⇒h=√a2−a22=a√22⇒a=h√2
⇒SABCD=a2=(h√2)2=2h2
Vậy VS.ABCD=13SO.SABCD=13h.2h2=2h33
Thể tích khối bát diện đều cạnh a bằng:
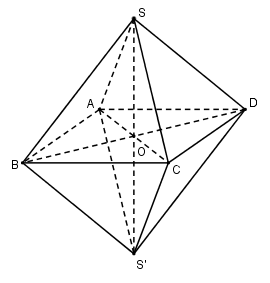
Thể tích khối bát diện đều V=2VS.ABCD
Gọi O=AC∩BD⇒SO⊥(ABCD)
Vì ABCD là hình vuông nên AC=BD=a√2⇒OA=12AC=a√22
SO⊥(ABCD)⇒SO⊥OA⇒ΔSOA vuông tại O⇒SO=√SA2−OA2=√a2−a22=a√22
⇒VS.ABCD=13SO.SABCD=13a√22.a2=a3√26
⇒V=2a3√26=a3√23
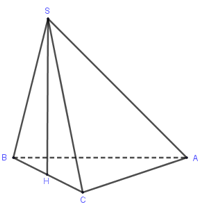
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A,AB=a,AC=a√3. Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
Trong mp(SBC) kẻ SH \bot BC\left( {H \in BC} \right) \Rightarrow SH \bot \left( {ABC} \right),H là trung điểm BC
Xét tam giác vuông ABC có BC = \sqrt {{a^2} + 3{a^2}} = 2a \Rightarrow \Delta SBC đều cạnh 2a
\Rightarrow SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{6}SH.AB.AC = \dfrac{1}{2}{a^3}
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Khoảng cách giữa hai đường thẳng SA và CD bằng a\sqrt 3 . Thể tích khối chóp S.ABCD là:
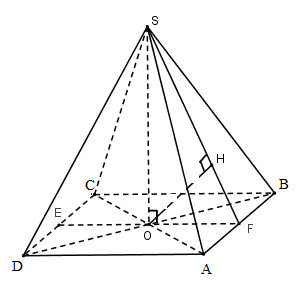
Gọi O = AC \cap BD. Vì chóp S.ABCD đều nên SO \bot \left( {ABCD} \right)
Gọi E và F lần lượt là trung điểm của CD và AB
Ta có:
\begin{array}{l}AB//CD \Rightarrow SA \subset \left( {SAB} \right)//CD\\ \Rightarrow d\left( {CD;SA} \right) = d\left( {CD;\left( {SAB} \right)} \right) = d\left( {E;\left( {SAB} \right)} \right) = 2d\left( {O;\left( {SAB} \right)} \right) = a\sqrt 3 \\ \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = \dfrac{{a\sqrt 3 }}{2}\end{array}
Ta có:
\left. \begin{array}{l}OF \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOF} \right)
Trong \left( {SOF} \right) kẻ OH \bot SF\,\,\left( 1 \right)
Vì AB \bot \left( {SOF} \right) \Rightarrow AB \bot OH\,\,\left( 2 \right)
Từ (1) và (2) suy ra OH \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH = \dfrac{{a\sqrt 3 }}{2}
Xét tam giác vuông SOF có: \dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{F^2}}}
\Rightarrow \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{O{F^2}}} = \dfrac{4}{{3{a^2}}} - \dfrac{1}{{{a^2}}} = \dfrac{1}{{3{a^2}}} \Rightarrow SO = a\sqrt 3
Vậy {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}a\sqrt 3 .4{a^2} = \dfrac{{4{a^3}\sqrt 3 }}{3}
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy \left( {ABCD} \right) và SA = a. Điểm M thuộc cạnh SA sao cho \dfrac{{SM}}{{SA}} = k. Xác định k sao cho mặt phẳng \left( {BMC} \right) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
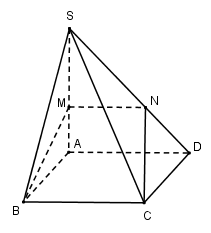
Vì BC//AD nên mặt phẳng \left( {BMC} \right) cắt \left( {SAD} \right) theo đoạn thẳng MN//AD\left( {N \in SD} \right)
Vì MN//AD \Rightarrow \dfrac{{SM}}{{SA}} = \dfrac{{SN}}{{SD}} = k
\begin{array}{l}\dfrac{{{V_{S.MBC}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}} = k \Rightarrow {V_{S.MBC}} = k.{V_{S.ABC}} = \dfrac{k}{2}.{V_{S.ABCD}}\\\dfrac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SD}} = {k^2} \Rightarrow {V_{S.MNC}} = {k^2}.{V_{S.ADC}} = \dfrac{{{k^2}}}{2}.{V_{S.ABCD}}\\ \Rightarrow {V_{S.MBCN}} = {V_{S.MBC}} + {V_{S.MNC}} = \left( {\dfrac{k}{2} + \dfrac{{{k^2}}}{2}} \right){V_{S.ABCD}}\end{array}
Để mặt phẳng \left( {BMNC} \right) chia hình chóp thành 2 phần có thể tích bằng nhau thì \dfrac{k}{2} + \dfrac{{{k^2}}}{2} = \dfrac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \dfrac{{ - 1 + \sqrt 5 }}{2} do k > 0.

