Phương trình đường tròn

Phương trình đường tròn $\left( C \right)$  tâm \(I\left( {a;b} \right)\), bán kính $R$ là :\({(x - a)^2} + {(y - b)^2} = {R^2}\)

Phương trình đường tròn ${x^2} + {y^2} - 2ax - 2by + c = 0$ có tâm \(I\left( {a;b} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} \).

Do đó: \(c = {a^2} + {b^2} - {R^2}\).

Phương trình ${x^2} + {y^2} + 2ax + 2by + c = 0{\rm{ }}$ với điều kiện ${a^2} + {b^2} - c > 0$, là phương trình đường tròn tâm \(I\left( { - a; - b} \right)\) bán kính \(R = \sqrt {{a^2} + {b^2} - c} \)

Do đó đáp án A sai.

Phương trình của đường tròn có tâm \(I( - 3;4)\) và bán kính \(R = 2\) là: \({(x + 3)^2} + {(y - 4)^2} = {2^2}\) hay\({(x + 3)^2} + {(y - 4)^2} - 4 = 0\)

\({x^2} + {y^2} + 2ax + 2by + c = 0,\) là phương trình đường tròn khi \({R^2} = {a^2} + {b^2} - c\). Điều này có nghĩa là \({a^2} + {b^2} - c > 0\)  hay \({a^2} + {b^2} > c\).

\({x^2} + {y^2} - 2\left( {m + 2} \right)x + 4my + 19m - 6 = 0\,\,\,\,\left( * \right)\)

(*) là phương trình đường tròn khi \({\left( {m + 2} \right)^2} + {\left( {2m} \right)^2} - 19m + 6 > 0 \Leftrightarrow 5{m^2} - 15m + 10 > 0\)\( \Leftrightarrow \) \(m < 1\) hoặc \(m > 2\)

Đáp án A: \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\) không phải là phương trình đường tròn vì hệ số của \(x^2\) là 1 và của \(y^2\) là 2.

Đáp án B: \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\) không phải là phương trình đường tròn vì hệ số của \(x^2\) là 4 và của \(y^2\) là 1.

Đáp án C: \({x^2} + {y^2} - 2x - 8y + 20 = 0\) có \(a = 1\,\,,b = 4,\,\,c = 20\).

Ta thấy \({a^2} + {b^2} =1^2+4^2=17 < 20 = c\). Đây không phải là một phương trình đường tròn.

Đáp án D: \({x^2} + {y^2} - 4x + 6y - 12 = 0\) có \(a = 2,\,\,b =  - 3,\,\,c =  - 12\).

Ta thấy \({a^2} + {b^2} =2^2+(-3)^2=13 > -12 = c\). Đây là một phương trình đường tròn.

\({x^2} + {y^2} - 2x + 4y + 1 = 0\) có hệ số \(a = 1,b =  - 2,c = 1\)  sẽ có tâm \(I\left( {1; - 2} \right)\) và \(R = \sqrt {{{\left( { - 1} \right)}^2} + {2^2} - 1}  = 2\)

\((C):{x^2} + {y^2} + 2x + 4y - 20 = 0\) có \(a =  - 1,\,\,b =  - 2,c =  - 20\) sẽ có tâm \(I\left( { - 1; - 2} \right)\) và bán kính \(R = \sqrt {{1^2} + {2^2} + 20}  = 5\). 

Thay tọa độ các điểm ở đáp án C và D vào phương trình đường tròn ta thấy hai đáp án đều đúng.

Suy ra mệnh đề sai là mệnh đề ở đáp án A.

Gọi đường tròn có phương trình ${x^2} + {y^2} + 2ax + 2by + c = 0\,\left( C \right)$

$A,\,B,\,C \in \left( C \right)$ $ \Leftrightarrow \left\{ \begin{array}{l}16 + 8b + c = 0\\20 + 4a + 8b + c = 0\\16 + 8a + c = 0\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b =  - 1\\c =  - 8\end{array} \right. \to I\left( {1;1} \right)$

\({x^2} + {y^2} = 1.\) Thay \(x = 0,y = 0\) ta có \({0^2} + {0^2} = 1\) là mệnh đề A sai.

\({x^2} + {y^2} - x - y + 2 = 0\). Thay \(x = 0,y = 0\) ta có \(2 = 0\) là mệnh đề B sai.

\({x^2} + {y^2} - 4x - 4y + 8 = 0.\) Thay \(x = 0,y = 0\) ta có \(8 = 0\) là mệnh đề C sai.

\({\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25.\) Thay \(x = 0,y = 0\) ta có \({\left( { - 3} \right)^2} + {\left( { - 4} \right)^2} = 25\) là mệnh đề đúng. Vậy \({\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25.\) đi qua gốc tọa độ.

Ta có: \(R = IA = \sqrt {{{\left( {1 - 2} \right)}^2} + {{\left( {3 + 4} \right)}^2}}  = \sqrt {50} \)

Phương trình đường tròn $(C)$ có tâm \(I\left( {2; - 4} \right)\)  có bán kính \(R = \sqrt {50} \) là: \({\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = 50.\)

\(\left( C \right):\left\{ \begin{array}{l}I\left( {0;0} \right)\\R = 1\end{array} \right. \) \( \to \left( C \right):{(x-0)^2} + {(y-0)^2} = 1 \) \(\to \left( C \right):{x^2} + {y^2} = 1.\)

Gọi $I$ là trung điểm của $AB.$

Khi đó \(\left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2} = \dfrac{{6 - 2}}{2} = 2\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{2 + 0}}{2} = 1\end{array} \right. \Rightarrow I\left( {2;1} \right)\)

Mặt khác \(R = \dfrac{{AB}}{2} = \dfrac{{\sqrt {{{\left( {6 + 2} \right)}^2} + {{\left( {2 - 0} \right)}^2}} }}{2} = \dfrac{{2\sqrt {17} }}{2} = \sqrt {17} \)

Khi đó, $(C)$ có dạng là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)

Giả sử điểm \(I({x_I};{y_I})\) là tâm của đường tròn $(C).$ Vì $I$ nằm trên đường thẳng \(x + y + 2 = 0\) nên ta có \({x_I} + {y_I} + 2 = 0\)   (1)

Vì đường tròn $(C)$ đi qua hai điểm \(A\left( {0;1} \right),\,\,B\left( {1;0} \right)\) nên ta có \(IA = IB\). Điều này tương đương với

\(I{A^2} = I{B^2}\)  hay

\(\begin{array}{l}{\left( {{x_I}} \right)^2} + {\left( {1 - {y_I}} \right)^2} = {\left( {1 - {x_I}} \right)^2} + {\left( {{y_I}} \right)^2}\\ \Leftrightarrow x_I^2 + y_I^2 - 2{y_I} + 1 = x_I^2 - 2{x_I} + 1 + y_I^2\\ \Leftrightarrow {x_I} = {y_I}\,\,\,\,\left( 2 \right)\end{array}\)

Từ $(1)$ và $(2)$ suy ra \({x_I} = {y_I} =  - 1\). Suy ra \(I\left( { - 1; - 1} \right)\).

Mặt khác ta có \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1 - 1} \right)}^2}}  = \sqrt 5 \) 

Vậy $(C)$ có dạng \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\)

Cách làm:

\({x^2} + {y^2} = 8\). Ta thay \(A(0;2)\) vào phương trình có \({0^2} + {2^2} = 8\) là mệnh đề sai. Loại A

\({x^2} + {y^2} + 2x + 4 = 0\). Ta thay \(A(0;2)\) vào phương trình có \({0^2} + {2^2} + 2.0 + 4 = 0\) là mệnh đề sai. Loại B

\({x^2} + {y^2} - 2x - 8 = 0\) Ta thay \(A(0;2)\) vào phương trình có \({0^2} + {2^2} - 2.0 - 8 = 0\) là mệnh đề sai. Loại C.

- Điểm $B$ thuộc \({d_1}:x + y + 5 = 0\) nên ta giả sử \(B(b; - b - 5)\)

Điểm $C$ thuộc \({d_2}:x + 2y - 7 = 0\) nên ta giả sử \(C(7 - 2c,c)\)

Vì tam giác $ABC$ có \(A(2;3)\), trọng tâm là $G(2; 0)$ nên ta có hệ phương trình

$\left\{ \begin{array}{l}2 + b + 7 - 2c = 6\\3 - b - 5 + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b - 2c =  - 3\\ - b + c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b =  - 1\end{array} \right.$

Suy ra \(B( - 1; - 4)\) và \(C(5;1)\)

- Giả sử phương trình đường tròn cần lập có dạng \({x^2} + {y^2} + 2ax + 2by + c = 0\). Vì đường tròn qua $3$ điểm  \(A(2;3)\), \(B( - 1; - 4)\) và \(C(5;1)\) nên ta có hệ phương trình:

\(\left\{ \begin{array}{l}4a + 6b + c =  - 13\\ - 2a - 8b + c =  - 17\\10a + 2b + c =  - 26\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{{ - 83}}{{54}}\\b = \dfrac{{17}}{{18}}\\c =  - \dfrac{{338}}{{27}}\end{array} \right.\)

Vậy phương trình đường tròn là:

$\begin{array}{l}
{x^2} + {y^2} + 2.\left( { - \frac{{83}}{{54}}} \right)x + 2.\left( {\frac{{17}}{{18}}} \right)y - \frac{{338}}{{27}} = 0\\
\Leftrightarrow {x^2} + {y^2} - \frac{{83}}{{27}}x + \frac{{17}}{9}y - \frac{{338}}{{27}} = 0
\end{array}$

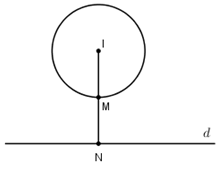
Đường tròn $(C )$ có tâm \(I( - 1;3)\) và bán kính \(R = \sqrt {{{\left( { - 1} \right)}^2} + {3^2} - 9}  = 1\).

Ta có: \(d(I;d) = \dfrac{{\left| {3.\left( { - 1} \right) - 4.3 + 5} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2 > R\)

Suy ra \(d\) không cắt $(C ).$

Ta có \(IM + MN \ge IN \Leftrightarrow MN \ge IN - R\)\(\) 

$MN $ min  \( \Leftrightarrow \)  $IN$ đạt min \( \Leftrightarrow \) $N$ là chân hình chiếu vuông góc của $I$ xuống đường thẳng $d.$

Giả sử \(N(a;b)\). Vì \(N \in d\) nên ta có $3a{\rm{  -  }}4b{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}0$ (1)

Mặt khác, ta có: $IN$ vuông góc với $d$ nên \(\overrightarrow {IN} .\overrightarrow {{u_d}}  = 0\). Mà \(\overrightarrow {IN}  = \left( {a + 1;b - 3} \right),\overrightarrow {{u_d}}  = \left( {4;3} \right)\). Suy ra ta có: \(4(a + 1) + 3(b - 3) = 0 \Leftrightarrow 4a + 3b - 5 = 0\)   (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}4a + 3b - 5 = 0\\3a - 4b + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{5}\\b = \dfrac{7}{5}\end{array} \right. \Rightarrow N\left( {\dfrac{1}{5};\dfrac{7}{5}} \right)\)

Vì \(d(I;d) = 2R\) nên \(M\) là trung điểm của \(IN\). Do đó, tọa độ của \(M\) là:

\(\left\{ \begin{array}{l}{x_M} = \dfrac{1}{2}\left( { - 1 + \dfrac{1}{5}} \right) =  - \dfrac{2}{5}\\{y_M} = \dfrac{1}{2}\left( {3 + \dfrac{7}{5}} \right) = \dfrac{{11}}{5}\end{array} \right. \Rightarrow M\left( { - \dfrac{2}{5};\dfrac{{11}}{5}} \right)\)

Đường tròn \(\left( {{C_m}} \right):\,\,{x^2} + {y^2} - 2mx + \left( {4m + 2} \right)y - 6m - 5 = 0\) có tâm \({I_m}\left( {m; - 2m - 1} \right)\)

Dễ thấy \(2{x_I} + {y_I} = 2.m + \left( { - 2m - 1} \right) =  - 1\)

Vậy \({I_m}\) thuộc đường thẳng \(2x + y =  - 1 \Leftrightarrow y =  - 2x - 1\)

Đường tròn \(({C_m}):{x^2} + {y^2} - 2mx - 4my - 5 = 0\) (\(m\) là tham số) có bán kính bằng 5

\( \Leftrightarrow {R^2} = {m^2} + 4{m^2} + 5 = 25\) \( \Leftrightarrow 5{m^2} = 20 \Leftrightarrow {m^2} = 4 \Leftrightarrow m =  \pm 2\)