Phương trình bậc nhất và bậc hai một ẩn

- Nếu  $a \ne 0$ thì phương trình có nghiệm \(x =  - \dfrac{b}{a}\).

- Nếu  $a = 0$ và \(b = 0\) thì phương trình có vô số nghiệm.

- Nếu  $a = 0$ và \(b \ne 0\) thì phương trình vô nghiệm.

Từ đó C đúng.

- TH1: Nếu \(a \ne 0\) thì phương trình có nghiệm duy nhất \( \Leftrightarrow \Delta  = 0\).

- TH2: Nếu \(a = 0\) thì phương trình trở thành \(bx + c = 0\) có nghiệm duy nhất \( \Leftrightarrow b \ne 0\).

Ta có:

${x^2} - \left( {2 + \sqrt 3 } \right)x + 2\sqrt 3  = 0$ $\Leftrightarrow \left( {{x^2} - 2x} \right) - \left( {\sqrt 3 x - 2\sqrt 3 } \right) = 0$ $\Leftrightarrow x\left( {x - 2} \right) - \sqrt 3 \left( {x - 2} \right) = 0$ $\Leftrightarrow \left( {x - 2} \right)\left( {x - \sqrt 3 } \right) = 0$ $\Leftrightarrow  \left[ \begin{array}{l}x = 2\\x = \sqrt 3 \end{array} \right.$

Vậy phương trình có hai nghiệm dương phân biệt.

Xét ${x^2} + m = 0$

Phương trình có nghiệm khi \(\Delta  \ge 0 \Leftrightarrow  - 4m \ge 0 \Leftrightarrow m \le 0\) .

Đáp án A: Nếu \(P < 0 \Rightarrow ac < 0\) nên phương trình có hai nghiệm trái dấu.

Đáp án B: Ta xét phương trình \({x^2} + x + 1 = 0\) có \(P = 1 > 0,S < 0\) nhưng lại vô nghiệm nên B sai.

Đáp án C, D: Nếu \(\Delta  > 0\) thì phương trình có hai nghiệm phân biệt. khi đó \(S,P\) lần lượt là tổng và tích hai nghiệm của phương trình. Do đó:

+) Nếu $P > 0$ và  $S < 0$ thì $\left( 1 \right)$ có $2$ nghiệm âm phân biệt.

+) Nếu $P > 0$ và  $S > 0$ thì $\left( 1 \right)$ có $2$ nghiệm dương phân biệt.

Phương trình có hai nghiệm âm phân biệt khi và chỉ khi  \(\left\{ \begin{array}{l}\Delta  > 0\\S < 0\\P > 0\end{array} \right.\) .

Ta có: $\left\{ \begin{array}{l}S = {x_1} + {x_2} = 2\\P = {x_1}.{x_2} =  - 1\end{array} \right.$$ \Rightarrow pt:{x^2} - Sx + P = 0 \Leftrightarrow {x^2} - 2x - 1 = 0$.

 Phương trình \(\left( {{m^2} - m} \right)x + m - 3 = 0\) là phương trình bậc nhất khi và chỉ khi:

\(a = {m^2} - m \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\m \ne 0\end{array} \right.\).

Xét đáp án A : Khi \(m = 2\) phương trình có dạng \(0.x + 0 = 0\) có vô số nghiệm nên A sai.

Xét đáp án B: Khi $m \ne 1$ thì \(m - 1 \ne 0\) nên phương trình $:\left( {m - 1} \right)x + 3m + 2 = 0$  có nghiệm duy nhất.

Xét đáp án C: Khi \(m = 2\) thì phương trình là:

\(\dfrac{{x - 2}}{{x - 2}} + \dfrac{{x - 3}}{x} = 3 \Leftrightarrow \dfrac{{x - 3}}{x} = 2 \Rightarrow x - 3 = 2x \Leftrightarrow x =  - 3\left( {TM} \right)\) nên C đúng.

Xét đáp án D: Khi $m \ne 2$ và $m \ne 0$ thì \({m^2} - 2m \ne 0\) nên phương trình $\left( {{m^2} - 2m} \right)x + m + 3 = 0\;$ có nghiệm.

Đáp án A: Phương trình: \(3x + 5 = 0\) có nghiệm là \(x =  - \dfrac{5}{3}\) nên A đúng.          

Phương trình: \(0x - 7 = 0\) vô nghiệm nên B đúng.                                             

Phương trình : \(0x + 0 = 0\) có vô số nghiệm hay có tập nghiệm \(\mathbb{R}\) nên C đúng.

Ta có: $\left( {a-3} \right)x + b = 2$ $ \Leftrightarrow \left( {a-3} \right)x + \left( {b - 2} \right) = 0$

Phương trình vô nghiệm khi $\left\{\begin{array}{l}a - 3=0\\b -2\ne 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b \ne 2\end{array} \right.$

Phương trình có nghiệm khi và chỉ khi:

$\left[ \begin{array}{l}{m^2}-2m \ne 0\\{m^2}-2m = {m^2}-3m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m \ne 0\\m \ne 2\end{array} \right.\\m = 2\end{array} \right. \Leftrightarrow m \ne 0$

Phương trình có vô số nghiệm khi $\left\{ \begin{array}{l}{m^2} - 3m + 2 = 0\\{m^2} + 4m + 5 = 0\end{array} \right. \Leftrightarrow m \in \emptyset $

(do phương trình \({m^2} + 4m + 5 = 0\) vô nghiệm với mọi \(m\)

Với \(m = 1\)  ta được phương trình \(3x - 1 = 0 \Leftrightarrow x = \dfrac{1}{3}\).

Với \(m \ne 1\).

\(\Delta ={3^2} + 4\left( {m - 1} \right)\)

Phương trình $\left( {m-1} \right){x^2}{\rm{ + }}3x-1 = 0$ có nghiệm khi \(\Delta  \ge 0\)\(\Leftrightarrow {3^2} + 4\left( {m - 1} \right) \ge 0 \Leftrightarrow m \ge  - \dfrac{5}{4}\).

Ta có:$\left( {x - 1} \right)\left( {{x^2} - 4mx - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 4mx - 4 = 0\end{array} \right.$

Phương trình có $3$ nghiệm phân biệt khi ${x^2} - 4mx - 4 = 0$ có $2$ nghiệm phân biệt khác $1$

$ \Leftrightarrow \left\{ \begin{array}{l}\Delta'  > 0\\f\left( 1 \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} + 4 > 0\\ - 4m - 3 \ne 0\end{array} \right. \Leftrightarrow m \ne  - \dfrac{3}{4}$.

- Xét phương trình $ - {x^2} - 2x + 3 = {x^2} - m \Leftrightarrow 2{x^2} + 2x - m - 3 = 0\left( 1 \right)$.

- Hai đồ thị có hai điểm chung khi và chỉ khi phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt

 $ \Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 + 2m + 6 > 0$$ \Leftrightarrow m >  - \dfrac{7}{2}$.

Gọi \({x_1},{x_2}\) là nghiệm của ${x^2}\; + {\rm{ }}px + {\rm{ }}q = 0$

Gọi \({x_3},{x_4}\) là nghiệm của ${x^2}\; + {\rm{ }}mx + {\rm{ }}n = 0$

- Khi đó, theo vi-et: \({x_1} + {x_2} =  - p\), \({x_3} + {x_4} =  - m\), \({x_3}.{x_4} = n\).

- Theo yêu cầu ta có:

$\left\{ \begin{array}{l}{x_1} = {x_3}^3\\{x_2} = {x_4}^3\end{array} \right.$$ \Rightarrow {x_1} + {x_2} = {x_3}^3 + {x_4}^3$$ \Leftrightarrow {x_1} + {x_2} = {\left( {{x_3} + {x_4}} \right)^3} - 3{x_3}{x_4}\left( {{x_3} + {x_4}} \right)$

$ \Rightarrow  - p =  - {m^3} + 3mn$$ \Rightarrow p = {m^3} - 3mn$.

Ta có: ${x^2} - 2a\left( {x-1} \right)-1 = 0$\( \Leftrightarrow {x^2} - 2ax + 2a - 1 = 0\) $ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2a - 1\end{array} \right.$(do \(1 + \left( { - 2a} \right) + 2a - 1 = 0\))

Yêu cầu bài toán ${x_1} + {x_2} = {x_1}^2 + {x_2}^2$$ \Rightarrow {x_1} + {x_2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}$

$ \Rightarrow 2a = 4{a^2} - 4a{\rm{ + 2}}$$ \Rightarrow \left[ \begin{array}{l}a = 1\\a = \dfrac{1}{2}\end{array} \right.$

Phương trình có hai nghiệm $\Leftrightarrow  \Delta ' = {\left( {m + 1} \right)^2} - \left( {{m^2} + 2} \right) = 2m + 1 \ge 0 $ $\Leftrightarrow m \ge \dfrac{1}{2}$

\(B = \sqrt {2\left( {x_1^2 + x_2^2} \right) + 16}  - 3{x_1}{x_2} = \sqrt {2{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2} + 16}  - 3{x_1}{x_2}\)

\( = \sqrt {2{{\left( {2m + 2} \right)}^2} - 4\left( {{m^2} + 2} \right) + 16}  - 3\left( {{m^2} + 2} \right) = \sqrt {4{m^2} + 16m + 16}  - 3\left( {{m^2} + 2} \right)\)

\( = 2m + 4 - 3\left( {{m^2} + 2} \right) =  - 3{m^2} + 2m - 2\)

Xét hàm số \(y =  - 3{m^2} + 2m - 2\)  với \(m \ge \dfrac{1}{2}\)

Bảng biến thiên

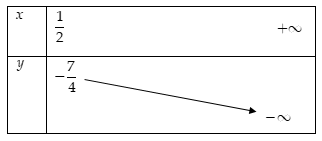
Suy ra giá trị \(\mathop {\max y}\limits_{m \ge \dfrac{1}{2}}  =  - \dfrac{7}{4}\) khi \(m = \dfrac{1}{2}\)

Vậy giá trị lớn nhất của biểu thức \(B\) là \( - \dfrac{7}{4}\) khi \(m = \dfrac{1}{2}\).

Gọi \({x_1};{x_2}\) là nghiệm của phương trình ${x^2}-2mx + 1 = 0\;$khi đó $\left\{ \begin{array}{l}\;{x_1} + {x_2} = 2m\\{x_1}.{x_2} = 1\end{array} \right.$

Gọi \({x_3};{x_4}\) là nghiệm của phương trình ${x^2}-2x + m = 0$ khi đó $\;\left\{ \begin{array}{l}{x_3} + {x_4} = 2\\{x_3}.{x_4} = m\end{array} \right.$

Ta có: $\left\{ \begin{array}{l}{x_1} = \dfrac{1}{{{x_3}}}\\{x_2} = \dfrac{1}{{{x_4}}}\end{array} \right.$$ \Rightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{1}{{{x_3}}} + \dfrac{1}{{{x_4}}}\\{x_1}.{x_2} = \dfrac{1}{{{x_3}.{x_4}}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{{x_3} + {x_4}}}{{{x_3}{x_4}}}\\{x_1}.{x_2} = \dfrac{1}{{{x_3}.{x_4}}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m = \dfrac{2}{m}\\1 = \dfrac{1}{m}\end{array} \right. \Leftrightarrow m = 1$