Khoảng cách từ một điểm đến một đường thẳng
Kỳ thi ĐGNL ĐHQG Hà Nội
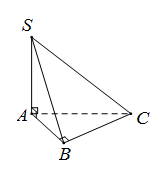
Cho hình chóp S.ABC trong đó SA,AB,BC đôi một vuông góc và SA=AB=BC=1. Khoảng cách giữa hai điểm S và C nhận giá trị nào trong các giá trị sau ?
Do {SA⊥ABSA⊥BC nên SA⊥(ABC)⇒SA⊥AC
Như vậy SC=√SA2+AC2=√SA2+AB2+BC2=√3
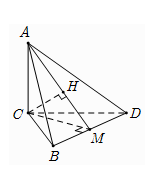
Cho hình chóp A.BCD có cạnh AC⊥(BCD) và BCD là tam giác đều cạnh bằng a. Biết AC=a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
Dựng hình chiếu H của C trên AM
Do ΔBCD đều cạnh a nên đường cao MC=a√32
d(C,AM)=CH=AC.MC√AC2+MC2=a√6611
Cho tứ diện SABC trong đóSA, SB, SC vuông góc với nhau từng đôi một vàSA=3a, SB=a,SC=2a. Khoảng cách từ A đến đường thẳng BC bằng:
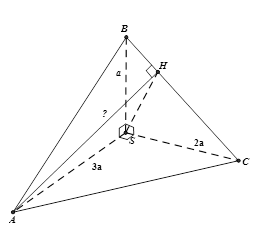
+ Dựng AH⊥BC ⇒d(A,BC)=AH.
+ {AS⊥(SBC)⊃BC⇒AS⊥BCAH⊥BC, AHcắt AS cùng nằm trong (SAH).
⇒BC⊥(SAH)⊃SH⇒BC⊥SH.
Xét trong ΔSBC vuông tại S có SH là đường cao ta có:
1SH2=1SB2+1SC2=1a2+14a2=54a2 ⇒SH2=4a25 ⇒SH=2a√55.
+ Ta dễ chứng minh được AS⊥(SBC)⊃SH⇒AS⊥SH ⇒ΔASH vuông tại S.
Áp dụng định lý Pi-ta-go cho ΔASH vuông tại Sta có:
AH2=SA2+SH2=9a2+4a25=49a25 ⇒AH=7a√55.
Cho hình chóp A.BCD có cạnh AC⊥(BCD) và BCD là tam giác đều cạnh bằng a. Biết AC=a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
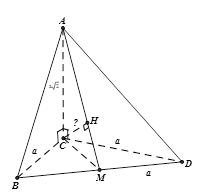
Dựng CH⊥AM⇒d(C,AM)=CH .
Vì ΔBCD là tam giác đều cạnh a và M là trung điểm của BD nên dễ tính được CM=a√32.
Xét ΔACM vuông tại C có CH là đường cao, ta có:
1CH2=1CA2+1CM2=12a2+13a24=116a2⇒CH2=6a211⇒CH=a√611
Hình chóp đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi H là trung điểm của BC, khoảng cách từ S đến AH bằng:
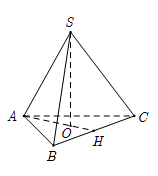
Gọi O là chân đường cao của hình chóp nên O là tâm tam giác đáy.
Do đó O là trọng tâm tam giác ABC hay O∈AH
Ta có AO=23AH=23.3a.√32=a√3
d(S,AH)=SO=√SA2−AO2=a
Cho hình chóp S.ABCDcó đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Khoảng cách từ M đến SA nhận giá trị nào trong các giá trị sau?

Ta có: SA⊥(ABCD)⇒SA⊥MA hay A là hình chiếu của M trên SA.
Khi đó d(M,SA)=MA=√AD2+DM2=√a2+a24=a√52
Cho hình chóp A.BCDcó cạnh AC⊥(BCD)và BCD là tam giác đều cạnh bằng a. Biết AC=a√2, khoảng cách từ A đến đường thẳng BD bằng:
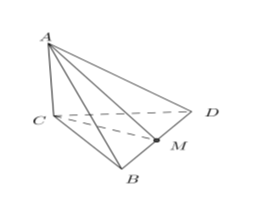
Gọi M là trung điểm của BD.
Ta có: {AC⊥BDCM⊥BD⇒BD⊥AM (Định lý 3 đường vuông góc) ⇒d(A;BD)=AM.
CM=a√32 (vì tam giác BCD đều).
Ta có: AM=√AC2+MC2=√2a2+3a24=a√112.
Cho hình chóp S.ABCDcó SA⊥(ABCD), đáy ABCD là hình thoi cạnh bằng a và ˆB=60∘. Biết SA=2a. Tính khoảng cách từ A đến SC.
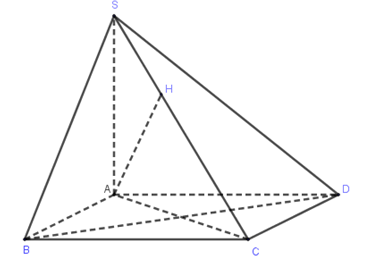
Kẻ AH⊥SC, khi đó d(A,SC)=AH.
ABCD là hình thoi cạnh bằng a và ˆB=60∘⇒ΔABC đều nên AC=a.
Trong tam giác vuông SACta có:
1AH2=1SA2+1AC2
⇒AH=SA.AC√SA2+AC2=2a.a√4a2+a2=2√5a5.
Cho hình chóp S.ABCD có SA⊥(ABCD), SA=2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
Kẻ OH⊥SC, khi đó d(O,SC)=OH. Ta có: ΔSAC∼ΔOHC(g−g) nên OHSA=OCSC⇒OH=OCSC.SA.
Mà: OC=12AC=a√22,SC=√SA2+AC2=a√6
Vậy OH=OCSC.SA=a√3=a√33
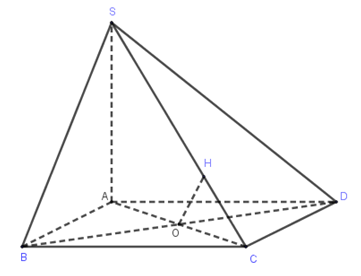
Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng α. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
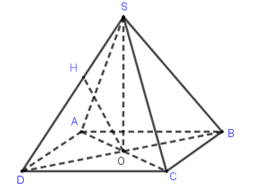
SO⊥(ABCD), O là tâm của hình vuông ABCD.
Kẻ OH⊥SD, khi đó d(O;SD)=OH,α=^SDO
OD=12BD=a√22 ⇒OH=ODsinα=a√2sinα2.
Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết SA=3a, AB=a√3, BC=a√6. Khoảng cách từ B đến SC bằng
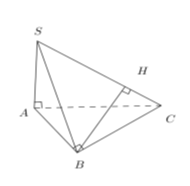
Vì SA,AB,BC vuông góc với nhau từng đôi một nên CB⊥SB.
Kẻ BH⊥SC, khi đó d(B;SC)=BH.
Ta có: SB=√SA2+AB2=√9a2+3a2=2√3a.
Trong tam giác vuông SBC ta có:
1BH2=1SB2+1BC2⇒BH=SB.BC√SB2+BC2=2a.
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD′ bằng
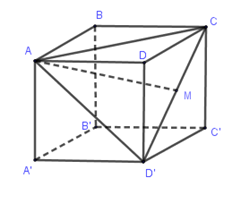
Gọi M là trung điểm của CD′. Do ABCD.A′B′C′D′là hình lập phương nên tam giác ACD′là tam giác đều cạnh a√2.
AM⊥CD′⇒d(A,CD′)=AM=a√62
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB′ bằng
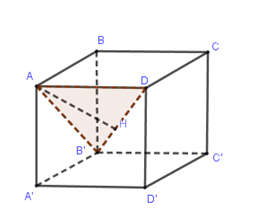
Gọi Hlà chân đường vuông góc hạ từ A xuống DB′.
Dễ thấy AD⊥(ABB′A′)⇒ΔADB′vuông đỉnh A.
Lại có AD=a;AB′=a√2⇒1AH2=1AD2+1AB′2⇒AH=a√63
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC′ bằng nhau ?
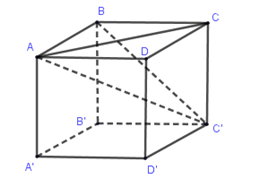
Dễ thấy các tam giác ABC′,C′CA,ADC′ là các tam giác vuông bằng nhau nên các đường cao hạ từ đỉnh góc vuông xuống cạnh huyền cũng bằng nhau.
Vậy: d(B,AC′)=d(C,AC′)=d(D,AC′)
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a√2. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng
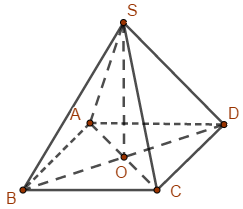
Bước 1:
Gọi O là giao điểm của AC và BD.
S.ABCD là hình chóp đều nên O là hình chiếu của S lên (ABCD).
=> d(S,(ABCD))=SO
Bước 2:
ABCD là hình vuông nên
AC=a√2.√2=2a=>AO=a=>SO2=SA2−AO2=2a2−a2=a2=>SO=a

