Câu hỏi:
3 năm trước
Cho hình chóp tứ giác đều có cạnh đáy bằng $a$ và góc hợp bởi một cạnh bên và mặt đáy bằng $\alpha $. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
Trả lời bởi giáo viên
Đáp án đúng: d
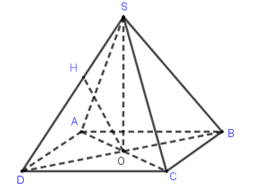
$SO \bot \left( {ABCD} \right)$, $O$ là tâm của hình vuông $ABCD$.
Kẻ $OH \bot SD$, khi đó $d\left( {O;SD} \right) = OH,\alpha = \widehat {SDO}$
$OD = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}$ $ \Rightarrow OH = OD\sin \alpha = \dfrac{{a\sqrt 2 \sin \alpha }}{2}$.
Hướng dẫn giải:
- Xác định góc giữa cạnh bên với đáy.
- Gọi \(O\) là tâm đáy, kẻ \(OH \bot SD\) và tính độ dài \(OH\) dựa vào các hệ thức lượng giác trong tam giác vuông.

