Cho hình chóp $A.BCD$ có cạnh $AC \bot \left( {BCD} \right)$ và $BCD$ là tam giác đều cạnh bằng $a$. Biết $AC = a\sqrt 2 $ và $M$ là trung điểm của $BD$. Khoảng cách từ $C$ đến đường thẳng $AM$ bằng
Trả lời bởi giáo viên
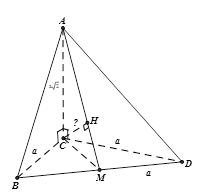
Dựng $CH \bot AM \Rightarrow d\left( {C,AM} \right) = CH$ .
Vì $\Delta BCD$ là tam giác đều cạnh $a$ và $M$ là trung điểm của $BD$ nên dễ tính được $CM = \dfrac{{a\sqrt 3 }}{2}$.
Xét $\Delta ACM$ vuông tại $C$ có $CH$ là đường cao, ta có:
$\begin{array}{l}\dfrac{1}{{C{H^2}}} = \dfrac{1}{{C{A^2}}} + \dfrac{1}{{C{M^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{1}{{\dfrac{{3{a^2}}}{4}}} = \dfrac{{11}}{{6{a^2}}}\\ \Rightarrow C{H^2} = \dfrac{{6{a^2}}}{{11}} \Rightarrow CH = a\sqrt {\dfrac{6}{{11}}} \end{array}$
Hướng dẫn giải:
- Dựng hình chiếu của \(C\) trên \(AM\).
- Tính khoảng cách dựa vào hệ thức giữa cạnh và đường cao trong tam giác vuông.

