Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?
Trả lời bởi giáo viên
Đáp án đúng: b
Do $\left\{ \begin{array}{l}SA \bot AB\\SA \bot BC\end{array} \right.$ nên $SA \bot (ABC) \Rightarrow SA \bot AC$
Như vậy \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {S{A^2} + A{B^2} + B{C^2}} = \sqrt 3 \)
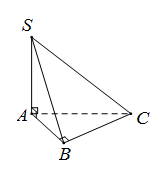
Hướng dẫn giải:
- Chứng minh \(SA \bot \left( {ABC} \right)\) rồi suy ra \(SA \bot AC\)
- Sử dụng định lý Pi-ta-go cho tam giác vuông \(SAC\)

