Câu hỏi:
3 năm trước
Cho hình chóp $A.BCD$có cạnh $AC \bot \left( {BCD} \right)$và $BCD$ là tam giác đều cạnh bằng $a$. Biết $AC = a\sqrt 2 $, khoảng cách từ $A$ đến đường thẳng $BD$ bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
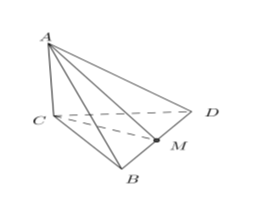
Gọi \(M\) là trung điểm của \(BD\).
Ta có: $\left\{ \begin{array}{l}AC \bot BD\\CM \bot BD\end{array} \right. \Rightarrow BD \bot AM$ (Định lý 3 đường vuông góc) $ \Rightarrow d\left( {A;BD} \right) = AM$.
$CM = \dfrac{{a\sqrt 3 }}{2}$ (vì tam giác $BCD$ đều).
Ta có: $AM = \sqrt {A{C^2} + M{C^2}} = \sqrt {2{a^2} + \dfrac{{3{a^2}}}{4}} = \dfrac{{a\sqrt {11} }}{2}$.
Hướng dẫn giải:
Gọi \(M\) là trung điểm của \(BD\) và chứng minh khoảng cách cần tìm là \(AM\).

