Câu hỏi:
3 năm trước
Hình chóp đều $S.ABC$ có cạnh đáy bằng $3a,$ cạnh bên bằng $2a$. Gọi \(H\) là trung điểm của \(BC\), khoảng cách từ $S$ đến \(AH\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
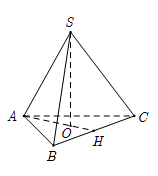
Gọi \(O\) là chân đường cao của hình chóp nên \(O\) là tâm tam giác đáy.
Do đó \(O\) là trọng tâm tam giác \(ABC\) hay \(O \in AH\)
Ta có \(AO = \dfrac{2}{3}AH = \dfrac{2}{3}.3a.\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)
${\rm{d}}\left( {S,AH} \right) = SO = \sqrt {S{A^2} - A{O^2}} = a$
Hướng dẫn giải:
- Dựng hình chiếu của \(S\) trên mặt đáy.
- Chứng minh khoảng cách cần tìm chính là khoảng cách từ \(S\) lên mặt đáy.

