Câu hỏi:
2 năm trước
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD′ bằng
Trả lời bởi giáo viên
Đáp án đúng: b
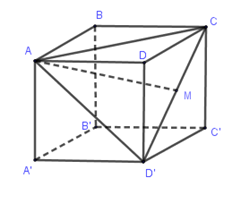
Gọi M là trung điểm của CD′. Do ABCD.A′B′C′D′là hình lập phương nên tam giác ACD′là tam giác đều cạnh a√2.
AM⊥CD′⇒d(A,CD′)=AM=a√62
Hướng dẫn giải:
Gọi M là trung điểm của CD′, chứng minh AM⊥CD′ và tính độ dài AM.

