Câu hỏi:
3 năm trước
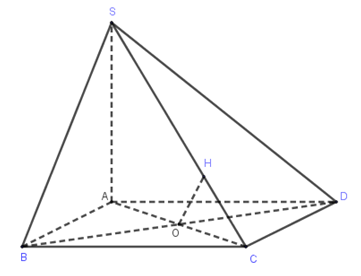
Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$, $SA = 2a$, $ABCD$ là hình vuông cạnh bằng $a$. Gọi $O$ là tâm của $ABCD$, tính khoảng cách từ $O$ đến $SC$.
Trả lời bởi giáo viên
Đáp án đúng: a
Kẻ $OH \bot SC$, khi đó $d\left( {O,SC} \right) = OH$. Ta có: $\Delta SAC \sim \Delta OHC(g-g)$ nên $\dfrac{{OH}}{{SA}} = \dfrac{{OC}}{{SC}} \Rightarrow OH = \dfrac{{OC}}{{SC}}.SA$.
Mà: $OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2},SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 6 $
Vậy $OH = \dfrac{{OC}}{{SC}}.SA = \dfrac{a}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3}$
Hướng dẫn giải:
Kẻ \(OH \bot SC\) và tính độ dài \(OH\) dựa vào tam giác đồng dạng và một số hệ thức giữa cạnh và đường coa trong tam giác vuông.

