Hàm số lũy thừa

Các hàm số ở mỗi đáp án A, B, D đều là hàm số lũy thừa.

- Hàm số $y = {x^\alpha }$ có TXĐ $D = R$ với mọi $\alpha$ nguyên dương nên A và B sai.

- Hàm số $y = {x^\alpha }$ có TXĐ $D = R\backslash \left\{ 0 \right\}$ với mọi $\alpha$ nguyên âm hoặc $\alpha  = 0$ nên C sai.

- Hàm số $y = {x^\alpha }$ có TXĐ $D = \left( {0; + \infty } \right)$ với mọi $\alpha$ không nguyên nên D đúng.

Vì hàm số $y = {x^{\frac{1}{n}}}$ có số mũ không nguyên nên cơ số phải dương, hay $x > 0$.

Ta có: $\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha  - 1}}$

Vì $\sqrt[n]{x} = {x^{\frac{1}{n}}}$ nếu $x > 0$ nên $\left( {\sqrt[n]{x}} \right)' = ({x^{\frac{1}{n}}})' = \dfrac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$ chỉ đúng nếu $x > 0$.

Hàm số $y = {x^\alpha }\left( {\alpha  \ne 0} \right)$ đồng biến trên $\left( {0; + \infty } \right)$ nếu $\alpha  > 0$ nên A và C sai.

Hàm số $y = {x^\alpha }\left( {\alpha  \ne 0} \right)$ nghịch biến trên $\left( {0; + \infty } \right)$ nếu $\alpha  < 0$ nên B đúng, D sai.

Với $\alpha  = 1$ thì $y = {x^1} = x$ nên đồ thị hàm số là đường thẳng.

Từ hình vẽ ta thấy $1 < {2^\alpha } < 2 \Rightarrow 0 < \alpha  < 1$

.

+ Hàm số $y = {x^{e - 3}}$ có $\alpha  = e - 3$ không nguyên, suy ra tập xác định là $\left( {0; + \infty } \right) \Rightarrow C$ đúng

+ Hàm số đi qua điểm $(1;1)$ suy ra A đúng

+ $y' = (e - 3).{x^{e - 4}} < 0,\forall x \in \left( {0; + \infty } \right) \Rightarrow B$ sai

+ Đồ thị hàm số có hai đường tiệm cận $Ox, Oy$ suy ra D đúng

Hàm số $y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}$ xác định khi ${x^3} - 27 > 0 \Leftrightarrow x > 3$.

Hàm số $y = {\left( {{x^4} - 3{x^2} - 4} \right)^{ - 2}}$ xác định khi ${x^4} - 3{x^2} - 4 \ne 0 \Leftrightarrow \left( {{x^2} + 1} \right)\left( {{x^2} - 4} \right) \ne 0 \Leftrightarrow {x^2} - 4 \ne 0 \Leftrightarrow x \ne  \pm 2$

$P = {x^{\frac{1}{3}}}\sqrt[6]{x} = {x^{\frac{1}{3}}}.{x^{\frac{1}{6}}} = {x^{\frac{1}{3} + \frac{1}{6}}} = {x^{\frac{1}{2}}} = \sqrt x$

Ta có:

$\begin{array}{l}{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} = {x^{1 + \dfrac{1}{{{{\log }_2}x}}}} = {x^{1 + {{\log }_x}2}} = {x^{{{\log }_x}2x}} = 2x\\{8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{3.\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{\dfrac{1}{{{{\log }_{{x^2}}}2}}}} = {2^{{{\log }_2}{x^2}}} = {x^2}\end{array}$

Khi đó $f\left( x \right) = {\left( {{x^2} + 2x + 1} \right)^{\dfrac{1}{2}}} - 1 = {\left( {{{\left( {x + 1} \right)}^2}} \right)^{\dfrac{1}{2}}} - 1 = x \Rightarrow f\left( x \right) = x$

Do đó $P = f\left( {f\left( {2018} \right)} \right) = f\left( {2018} \right) = 2018$.

Ta có:

$y' = \left[ {{{\left( {2{x^2} + x - 1} \right)}^{\dfrac{2}{3}}}} \right]' = \dfrac{2}{3}{\left( {2{x^2} + x - 1} \right)^{ - \dfrac{1}{3}}}\left( {2{x^2} + x - 1} \right)'$

$= \dfrac{2}{3}.\dfrac{1}{{\sqrt[3]{{2{x^2} + x - 1}}}}\left( {4x + 1} \right) = \dfrac{{2\left( {4x + 1} \right)}}{{3\sqrt[3]{{2{x^2} + x - 1}}}}$

TXĐ: $D = \left( { - \infty ; - 2} \right) \cup \left( {1; + \infty } \right)$

Ta có:

$y' = f'\left( x \right) = \left[ {{{\left( {{x^2} + x - 2} \right)}^{\dfrac{2}{3}}}} \right]' = \dfrac{2}{3}{\left( {{x^2} + x - 2} \right)^{ - \dfrac{1}{3}}}\left( {{x^2} + x - 2} \right)'$

$= \dfrac{2}{3}{\left( {{x^2} + x - 2} \right)^{ - \dfrac{1}{3}}}\left( {2x + 1} \right) = \dfrac{{2\left( {2x + 1} \right)}}{{3\sqrt[3]{{{x^2} + x - 2}}}},\forall x \in D$.

Do đó:

$f'\left( 2 \right) = \dfrac{{10}}{{3\sqrt[3]{4}}};f'\left( { - 3} \right) =  - \dfrac{{10}}{{3\sqrt[3]{4}}};f'\left( 3 \right) = \dfrac{{14}}{{3\sqrt[3]{{10}}}}$  và không tồn tại $f'\left( 0 \right)$.

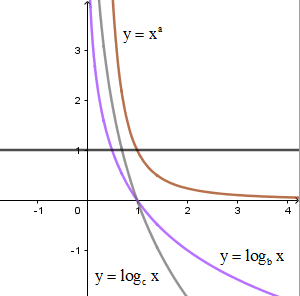
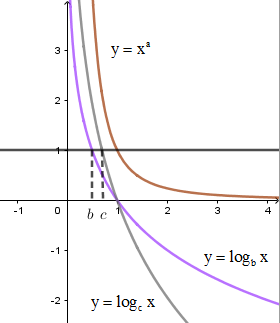
Ta thấy hàm số $y = {x^a}$ nghịch biến nên $a < 0$ nên loại C, D.

Kẻ đường thẳng $y = 1$ cắt hai đồ thị hàm số $y = {\log _b}x;y = {\log _c}x$ tại hai điểm lần lượt có hoành độ $x = b;x = c$. Quan sát đồ thị ta thấy $b < c$.

Vậy $a < b < c$.

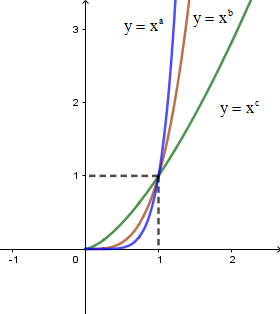
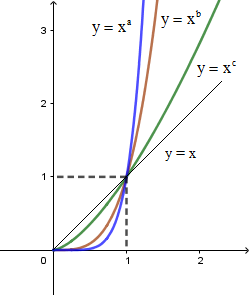
Từ đồ thị hàm số ta thấy:

- Với $0 < x < 1$ thì ${x^a} < {x^b} < {x^c} < {x^1} \Leftrightarrow a > b > c > 1$

- Với $x > 1$ thì $x < {x^c} < {x^b} < {x^a} \Rightarrow 1 < c < b < a$

Vậy $1 < c < b < a$

Ta có:

$\begin{array}{l}y' =  - 2.{\left( {x + 2} \right)^{ - 3}}.\left( {x + 2} \right)' =  - 2{\left( {x + 2} \right)^{ - 3}}\\y'' =  - 2.\left( { - 3} \right).{\left( {x + 2} \right)^{ - 4}}\left( {x + 2} \right)' = 6{\left( {x + 2} \right)^{ - 4}}\\ \Rightarrow y'' = 6{y^2}\\ \Leftrightarrow y'' - 6{y^2} = 0\end{array}$

Đồ thị hàm số không có tiệm cận là $y = {x^{\frac{1}{3}}}$.

Ta có: $y' = \dfrac{\pi }{2}{x^{\frac{\pi }{2} - 1}} \Rightarrow y'\left( 1 \right) = \dfrac{\pi }{2}$.

Với ${x_0} = 1$ thì ${y_0} = {1^{\frac{\pi }{2}}} = 1$.

Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm ${M_0}$ là: $y = \dfrac{\pi }{2}\left( {x - 1} \right) + 1 = \dfrac{\pi }{2}x - \dfrac{\pi }{2} + 1$.