Phép chiếu song song trong không gian

Qua phép chiếu song song, tính chất chéo nhau không được bảo toàn.

Khi phương chiếu $l$ thỏa mãn $\left( \alpha  \right)//l$ hoặc $\left( \alpha  \right) \supset l$ thì các đoạn thẳng $AB$,$BC$,$CA$ có hình chiếu lên $\left( P \right)$ nằm trên giao tuyến của $\left( \alpha  \right)$ và $\left( P \right)$.

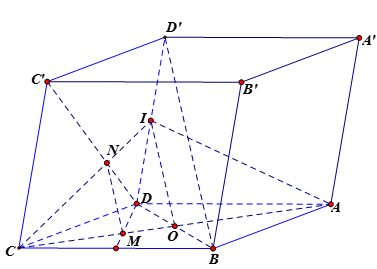
Ta có: \(M\)là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Nên \(M\) là trọng tâm của tam giác \(BCD\).

Gọi \(O\) và \(I\) lần lượt là trung điểm của \(AC\) và \(DD'\). Khi đó ta có: \(BD'\;{\rm{//}}\;\left( {IAC} \right)\).

Trong \(\left( {CDD'C'} \right)\), gọi \(N' = CI \cap C'D\). Suy ra \(N'\) là trọng tâm tam giác \(CDD'\).

Do đó: \(\dfrac{{CM}}{{CO}} = \dfrac{2}{3} = \dfrac{{CN'}}{{CI}}\) \( \Rightarrow MN'\;{\rm{//}}\;OI\), mà \(OI\;{\rm{//}}\;BD'\) nên \(MN'\;{\rm{//}}\;BD'\).

Vậy \(N' \equiv N\) và \(x = \dfrac{2}{3}\).

Phép chiếu song song biến hai đường thẳng song song thành đường thẳng song song hặc trùng nhau.

Hình chiếu của một điểm nằm trên mặt phẳng qua phép chiếu song song lên mặt phẳng đó là chính điểm đó.

Hình chiếu của đường thẳng qua phép chiếu song song theo phương song song với đường thẳng đó trên mặt phẳng chiếu là một điểm. Điểm đó là giao điểm của đường thẳng và mặt phẳng.

Vì \(M'\) là hình chiếu của  nên \(MM'//l\) nên A đúng.

Lại có \(l \bot \left( \alpha  \right) \Rightarrow MM' \bot \left( \alpha  \right)\) nên C đúng, B sai.

Hiển nhiên \(M' \in \left( \alpha  \right)\) nên D đúng.

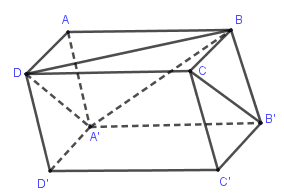
Xét phép chiếu theo song song theo phương \(CB'\) lên mặt phẳng \(\left( {ABD} \right)\).

Ta có: \(B \in \left( {ABD} \right)\) nên hình chiếu của \(B\) qua phép chiếu là chính nó.

Lại có: \(A'D//CB'\) nên hình chiếu của \(A'\) qua phép chiếu là điểm \(D\).

Do đó hình chiếu của \(A'B\) qua phép chiếu là \(BD\).

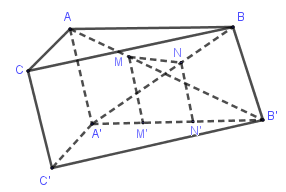
Qua \(M\) kẻ đường thẳng song song với \(AA'\) cắt \(A'B'\) tại \(MM' \Rightarrow MM'//AA'//CC'\) nên \(M'\) là hình chiếu của \(M\) qua phép chiếu bài cho.

Tương tự \(N' \in A'B'\) mà \(NN'//BB'\) cũng là ảnh của \(N\) qua phép chiếu bài cho.

Khi đó \(M'N' \subset A'B',MM'//AA',M'N'//AB\) nên các đáp án B, C, D đều đúng.

Đáp án A sai vì \(MN\) và \(M'N'\) không song song.

Do phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau, nên không thể có đáp án A.

Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước ( hình vuông, hình thoi, hình chữ nhật, hình bình hành…)

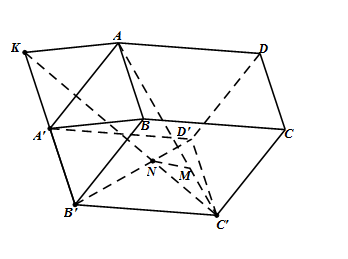
Xét phép chiếu song song lên mặt phẳng $\left( {A'B'C'D'} \right)$ theo phương chiếu $BA'$. Ta có $N$ là ảnh của $M$ hay $N$ chính là giao điểm của $B'D'$ và ảnh $AC'$ qua phép chiếu này.

Do đó ta xác định $M,N$ như sau:

Trên $A'B'$ kéo dài lấy điểm $K$ sao cho $A'K = B'A'$ thì $ABA'K$ là hình bình hành nên $AK//BA'$ suy ra $K$ là ảnh của $A$ trên $(A'B'C'D')$ qua phép chiếu song song theo phương \(BA'\).

Gọi $N = B'D' \cap KC'$. Đường thẳng qua $N$ và song song với $AK$ cắt $AC'$ tại $M$. Ta có $M,N$ là các điểm cần xác định.

Theo định lí Thales, ta có $\dfrac{{MA}}{{MC'}} = \dfrac{{NK}}{{NC'}} = \dfrac{{KB'}}{{C'D'}} = 2$.

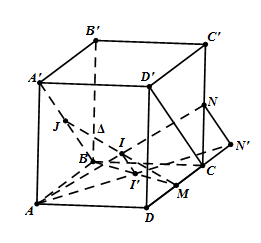
Xét phép chiếu song song lên $\left( {ABCD} \right)$theo phương chiếu $A'B$. Khi đó ba điểm $J,I,M$ lần lượt có hình chiếu là $B,I',M$. Do $J,I,M$ thẳng hàng nên $B,I',M$ cũng thẳng hàng. Gọi $N'$ là hình chiếu của $N$ thì $AN'$ là hình chiếu của $AN$. Vì $I \in AN \Rightarrow I' \in AN' \Rightarrow I' = BM \cap AN'$.

Từ phân tích trên suy ra cách dựng:

Lấy $I' = AN' \cap BM$.

Trong $\left( {ANN'} \right)$ dựng $II'\parallel NN'$( đã có $NN'\parallel CD'$) cắt $AN$ tại $I$.

Vẽ đường thẳng $MI$, đó chính là đường thẳng cần dựng.

Ta có $MC = CN'$ suy ra $MN' = CD = AB$. Do đó $I'$ là trung điểm của $BM$. Mặt khác $II'\parallel JB$ nên $II'$ là đường trung bình của tam giác $MBJ$, suy ra $IM = IJ \Rightarrow \dfrac{{IM}}{{IJ}} = 1$.

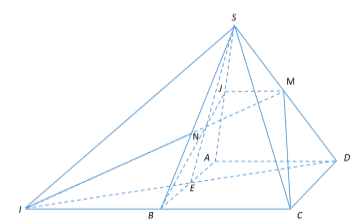
Gọi \(J;E\) lần lượt là trung điểm $SA;AB$.

Trong mặt phẳng \(\left( {BCMJ} \right)\) gọi \(I = MN \cap BC\).

• Ta có: \(IM\) là đường trung tuyến của tam giác \(SID\).
• Trong tam giác \(ICD\) ta có \(BE\) song song và bằng \(\dfrac{1}{2}CD\) nên suy ra \(BE\) là đường trung bình của tam giác \(ICD \Rightarrow E\) là trung điểm \(ID \Rightarrow SE\) là đường trung tuyến của tam giác \(SID\).

Ta có: \(N = IM \cap SE \Rightarrow N\) là trọng tâm tam giác \(SID \Rightarrow \dfrac{{IN}}{{IM}} = \dfrac{2}{3}\).

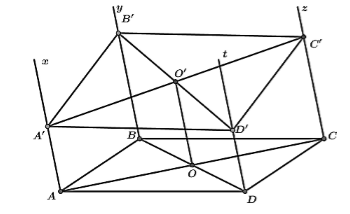
Do \(\left( P \right)\) cắt mặt phẳng $\left( {Ax,By} \right)$ theo giao tuyến \(A'B'\); cắt mặt phẳng $\left( {Cz,Dt} \right)$ theo giao tuyến \(C'D'\), mà hai mặt phẳng $\left( {Ax,By} \right)$ và $\left( {Cz,Dt} \right)$ song song nên \(A'B'{\rm{//}}C'D'\).

Tương tự có \(A'D'{\rm{//}}B'C'\) nên \(A'B'C'D'\) là hình bình hành.

Gọi \(O\), \(O'\) lần lượt là tâm \(ABCD\) và \(A'B'C'D'\). Dễ dàng có $OO'$ là đường trung bình của hai hình thang $AA'C'C$ và \(BB'D'D\) nên \(OO' = \dfrac{{AA' + CC'}}{2} = \dfrac{{BB' + DD'}}{2}\).

Từ đó ta có \(DD' = 2\).

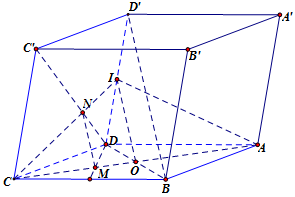
Ta có: \(M\) là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Nên \(M\) là trọng tâm của tam giác \(BCD\).

Gọi \(O\) và \(I\) lần lượt là trung điểm của \(AC\) và \(DD'\). Khi đó ta có: \(BD'\;{\rm{//}}\;\left( {IAC} \right)\).

Trong \(\left( {CDD'C'} \right)\), gọi \(N' = CI \cap C'D\). Suy ra \(N'\) là trọng tâm tam giác \(CDD'\).

Do đó: \(\dfrac{{CM}}{{CO}} = \dfrac{2}{3} = \dfrac{{CN'}}{{CI}}\) \( \Rightarrow MN'\;{\rm{//}}\;OI\), mà \(OI\;{\rm{//}}\;BD'\) nên \(MN'\;{\rm{//}}\;BD'\).

Vậy \(N' \equiv N\) và \(x = \dfrac{2}{3}\)