Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\) là trung điểm \(SD\), \(N\) là trọng tâm tam giác \(SAB\). Đường thẳng \(MN\) cắt mặt phẳng \(\left( {SBC} \right)\) tại điểm \(I\). Tính tỷ số \(\dfrac{{IN}}{{IM}}\).
Trả lời bởi giáo viên
Đáp án đúng: d
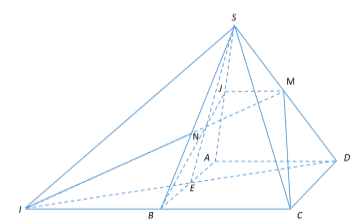
Gọi \(J;E\) lần lượt là trung điểm $SA;AB$.
Trong mặt phẳng \(\left( {BCMJ} \right)\) gọi \(I = MN \cap BC\).
- Ta có: \(IM\) là đường trung tuyến của tam giác \(SID\).
- Trong tam giác \(ICD\) ta có \(BE\) song song và bằng \(\dfrac{1}{2}CD\) nên suy ra \(BE\) là đường trung bình của tam giác \(ICD \Rightarrow E\) là trung điểm \(ID \Rightarrow SE\) là đường trung tuyến của tam giác \(SID\).
Ta có: \(N = IM \cap SE \Rightarrow N\) là trọng tâm tam giác \(SID \Rightarrow \dfrac{{IN}}{{IM}} = \dfrac{2}{3}\).
Hướng dẫn giải:
Dựng hình và tính tỉ số dựa vào các kiến thức hình học đã biết.

