Câu hỏi:
2 năm trước
Cho hình bình hành \(ABCD\). Qua \(A\), \(B\), \(C\), \(D\) lần lượt vẽ các nửa đường thẳng $Ax$, \(By\), \(Cz\), \(Dt\) ở cùng phía so với mặt phẳng \(\left( {ABCD} \right)\), song song với nhau và không nằm trong \(\left( {ABCD} \right)\). Một mặt phẳng \(\left( P \right)\) cắt $Ax$, \(By\), \(C{\rm{z}}\), \(Dt\) tương ứng tại \(A'\), \(B'\), \(C'\), \(D'\) sao cho $AA' = 3$, \(BB' = 5\), \(CC' = 4\). Tính $DD'$.
Trả lời bởi giáo viên
Đáp án đúng: c
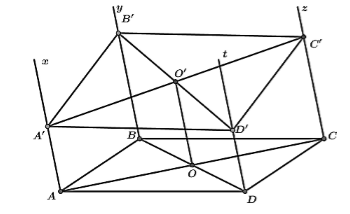
Do \(\left( P \right)\) cắt mặt phẳng $\left( {Ax,By} \right)$ theo giao tuyến \(A'B'\); cắt mặt phẳng $\left( {Cz,Dt} \right)$ theo giao tuyến \(C'D'\), mà hai mặt phẳng $\left( {Ax,By} \right)$ và $\left( {Cz,Dt} \right)$ song song nên \(A'B'{\rm{//}}C'D'\).
Tương tự có \(A'D'{\rm{//}}B'C'\) nên \(A'B'C'D'\) là hình bình hành.
Gọi \(O\), \(O'\) lần lượt là tâm \(ABCD\) và \(A'B'C'D'\). Dễ dàng có $OO'$ là đường trung bình của hai hình thang $AA'C'C$ và \(BB'D'D\) nên \(OO' = \dfrac{{AA' + CC'}}{2} = \dfrac{{BB' + DD'}}{2}\).
Từ đó ta có \(DD' = 2\).
Hướng dẫn giải:
- Gọi \(O,O'\) là tâm các hình bình hành \(ABCD,A'B'C'D'\)
- Tính \(OO'\) và suy ra \(DD'\) với chú ý \(OO'\) là đường trung bình các hình thang \(ACC'A',BB'D'D\)
