Câu hỏi:
2 năm trước
Cho hình hộp $ABCD.A'B'C'D'$. Gọi $M,N$ lần lượt là trung điểm của $CD$ và $CC'$. Kẻ đường thẳng $\Delta $ đi qua $M$ đồng thời cắt $AN$ và $A'B$ tại $I,J$. Hãy tính tỉ số $\dfrac{{IM}}{{IJ}}$.
Trả lời bởi giáo viên
Đáp án đúng: d
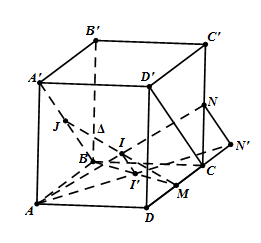
Xét phép chiếu song song lên $\left( {ABCD} \right)$theo phương chiếu $A'B$. Khi đó ba điểm $J,I,M$ lần lượt có hình chiếu là $B,I',M$. Do $J,I,M$ thẳng hàng nên $B,I',M$ cũng thẳng hàng. Gọi $N'$ là hình chiếu của $N$ thì $AN'$ là hình chiếu của $AN$. Vì $I \in AN \Rightarrow I' \in AN' \Rightarrow I' = BM \cap AN'$.
Từ phân tích trên suy ra cách dựng:
Lấy $I' = AN' \cap BM$.
Trong $\left( {ANN'} \right)$ dựng $II'\parallel NN'$( đã có $NN'\parallel CD'$) cắt $AN$ tại $I$.
Vẽ đường thẳng $MI$, đó chính là đường thẳng cần dựng.
Ta có $MC = CN'$ suy ra $MN' = CD = AB$. Do đó $I'$ là trung điểm của $BM$. Mặt khác $II'\parallel JB$ nên $II'$ là đường trung bình của tam giác $MBJ$, suy ra $IM = IJ \Rightarrow \dfrac{{IM}}{{IJ}} = 1$.
Hướng dẫn giải:
- Dựng hai điểm \(I,J\) bằng cách sửa dụng phép chiếu song song theo phương \(A'B\) tới mặt phẳng \(ABCD\).
Ảnh của $M$ và $J$ lần lượt là $M$ và $B$ và \(\Delta \subset (A'BM)\). Do đó $I$ là giao điểm của $(A'BM)$ và $AN$.
$MI$ cắt $A'B$ tại $J$.
- Sử dụng tính chất đường trung bình của tam giác để tính tỉ số \(\dfrac{{IM}}{{IJ}}\).
