Câu hỏi:
2 năm trước
Cho hình hộp $ABCD.A'B'C'D'$. Gọi các điểm $M,N$ tương ứng trên các đoạn $AC',B'D'$ sao cho $MN$ song song với $BA'$. Tỉ số $\dfrac{{MA}}{{MC'}}$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
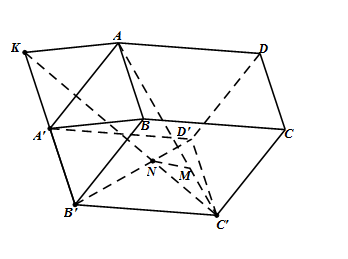
Xét phép chiếu song song lên mặt phẳng $\left( {A'B'C'D'} \right)$ theo phương chiếu $BA'$. Ta có $N$ là ảnh của $M$ hay $N$ chính là giao điểm của $B'D'$ và ảnh $AC'$ qua phép chiếu này.
Do đó ta xác định $M,N$ như sau:
Trên $A'B'$ kéo dài lấy điểm $K$ sao cho $A'K = B'A'$ thì $ABA'K$ là hình bình hành nên $AK//BA'$ suy ra $K$ là ảnh của $A$ trên $(A'B'C'D')$ qua phép chiếu song song theo phương \(BA'\).
Gọi $N = B'D' \cap KC'$. Đường thẳng qua $N$ và song song với $AK$ cắt $AC'$ tại $M$. Ta có $M,N$ là các điểm cần xác định.
Theo định lí Thales, ta có $\dfrac{{MA}}{{MC'}} = \dfrac{{NK}}{{NC'}} = \dfrac{{KB'}}{{C'D'}} = 2$.
Hướng dẫn giải:
- Tìm ảnh của \(AC'\) qua phép chiếu song song theo phương \(BA'\) trên mặt phẳng \(\left( {A'B'C'D'} \right)\).
- Điểm \(N\) là giao điểm của hình chiếu vừa tìm được với \(B'D'\).
- Qua \(N\) kẻ đường thẳng song song với \(BA'\) cắt \(AC'\) tại \(M\).
- Sử dụng định lý Ta-let để tính tỉ số \(\dfrac{{MA}}{{MC'}}\).
