Cho lăng trụ tam giác \(ABC.A'B'C'\), gọi \(M,N\) lần lượt là hai điểm bất kỳ phân biệt nằm trên các cạnh \(AB',A'B\). Hình chiếu của chúng qua phép chiếu song song theo phương \(CC'\) trên mặt phẳng \(\left( {A'B'C'} \right)\) lần lượt là \(M',N'\). Chọn kết luận không đúng:
Trả lời bởi giáo viên
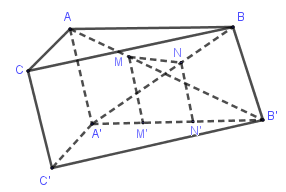
Qua \(M\) kẻ đường thẳng song song với \(AA'\) cắt \(A'B'\) tại \(MM' \Rightarrow MM'//AA'//CC'\) nên \(M'\) là hình chiếu của \(M\) qua phép chiếu bài cho.
Tương tự \(N' \in A'B'\) mà \(NN'//BB'\) cũng là ảnh của \(N\) qua phép chiếu bài cho.
Khi đó \(M'N' \subset A'B',MM'//AA',M'N'//AB\) nên các đáp án B, C, D đều đúng.
Đáp án A sai vì \(MN\) và \(M'N'\) không song song.
Hướng dẫn giải:
- Xác định các điểm \(M',N'\) dựa và định nghĩa phép chiếu song song và tính chất lăng tru.
- Xét tính đúng sai của các đáp án đã cho dựa vào quan hệ song song.

