Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Khoảng cách từ đỉnh \(A\) của hình lập phương đó đến đường thẳng \(DB'\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
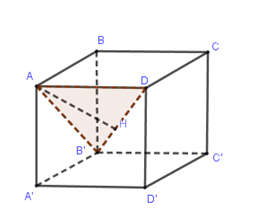
Gọi $H$là chân đường vuông góc hạ từ $A$ xuống $DB'$.
Dễ thấy $AD \bot \left( {ABB'A'} \right) \Rightarrow \Delta ADB'$vuông đỉnh $A$.
Lại có $AD = a;AB' = a\sqrt 2 \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{AB{'^2}}} \Rightarrow AH = \dfrac{{a\sqrt 6 }}{3}$
Hướng dẫn giải:
Kẻ \(AH \bot B'D\) và tính độ dài \(AH\).

