Câu hỏi:
3 năm trước
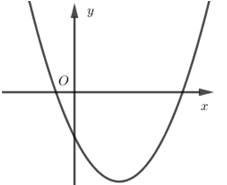
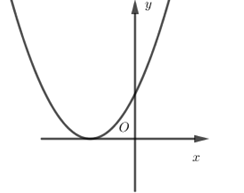
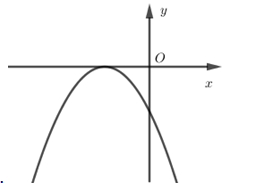
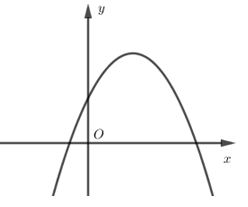
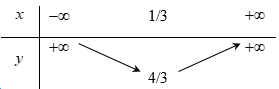
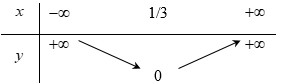
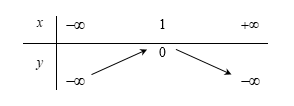
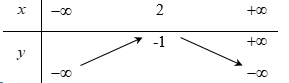
Nếu hàm số $y = a{x^2} + bx + c$ có $a < 0,b > 0$ và $c > 0$ thì đồ thị của nó có dạng:
Trả lời bởi giáo viên
Đáp án đúng: d
+ \(a < 0\) nên loại đáp án A,B.
+ \(c > 0\) nên giao điểm của đồ thị với trục tung có tung độ dương, chọn đáp án D.
Ngoài ra các em cũng có thể nhận xét vì \(b > 0,a < 0\) nên hoành độ đỉnh \( - \dfrac{b}{{2a}} > 0\) và đáp án D thỏa mãn.
Hướng dẫn giải:
- Từ \(a < 0\) suy ra dáng đồ thị và loại đáp án.
- Từ \(c > 0\) suy ra giao điểm của đồ thị với trục tung có tung độ dương.