Câu hỏi:
2 năm trước
Hàm số nào sau đây nghịch biến trong khoảng \(\left( { - \infty ;\,0} \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: a
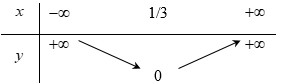
Đáp án A: \(a = \sqrt 2 > 0\) và \( - \dfrac{b}{{2a}} = 0\) nên hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\)
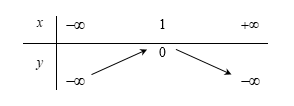
Đáp án B: \(a = - \sqrt 2 < 0\) và \( - \dfrac{b}{{2a}} = 0\) nên hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
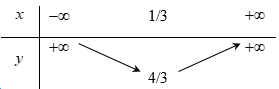
Đáp án C: \(y = \sqrt 2 \left( {{x^2} + 2x + 1} \right) = \sqrt 2 {x^2} + 2\sqrt 2 x + \sqrt 2 \) có \(a = \sqrt 2 > 0\) và \( - \dfrac{b}{{2a}} = - 1\) nên hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) nhưng \(\left( { - \infty ;0} \right) \not\subset \left( { - \infty ; - 1} \right)\) nên hàm số không nghịch biến trên \(\left( { - \infty ;0} \right)\)
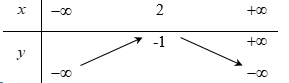
Đáp án D: \(y = - \sqrt 2 \left( {{x^2} + 2x + 1} \right) = - \sqrt 2 {x^2} - 2\sqrt 2 x - \sqrt 2 \) có \(a = - \sqrt 2 < 0\) và \( - \dfrac{b}{{2a}} = - 1\) nên hàm số nghịch biến trên \(\left( { - 1; + \infty } \right)\)
Vậy chỉ có đáp án A đúng.
Hướng dẫn giải:
Sử dụng tính đơn điệu của hàm số bậc hai.
- Nếu \(a > 0\) thì hàm số đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\), đạt được GTNN trên \(R\) tại \(x = - \dfrac{b}{{2a}}\).
- Nếu \(a < 0\) thì hàm số nghịch biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\), đồng biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\), đạt được GTLN trên \(R\) tại \(x = - \dfrac{b}{{2a}}\).
