Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA = x$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Xác định $x$ để hai mặt phẳng $\left( {SBC} \right)$ và $\left( {SCD} \right)$ tạo với nhau một góc ${60^0}.$
Trả lời bởi giáo viên
Đáp án đúng: c
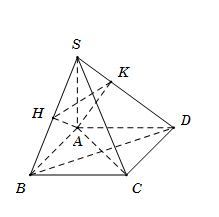
Từ $A$ kẻ $AH$ vuông góc với $SB\,\,\,\,\left( {H \in SB} \right).$
Ta có $\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH$ mà $AH \bot SB$ suy ra $AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$
Từ A kẻ AK vuông góc với $SD\,\,\,\left( {K \in SD} \right),$ tương tự, chứng minh được $AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC$
Khi đó $SC \bot \left( {AHK} \right)$ suy ra
$\widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK} = {60^0}.$
Lại có $\Delta \,SAB = \Delta \,SAD\,\,\left( {c.g.c} \right) \Rightarrow AH = AK$ mà $\widehat {HAK} = {60^0}$ suy ra tam giác AHK đều.
Tam giác SAB vuông tại A có $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{a^2}}} \Rightarrow AH = \dfrac{{xa}}{{\sqrt {{x^2} + {a^2}} }} = AK = HK$
Suy ra $SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{x^2} - \dfrac{{{x^2}{a^2}}}{{{x^2} + {a^2}}}} = \dfrac{{{x^2}}}{{\sqrt {{x^2} + {a^2}} }} \Rightarrow \dfrac{{SH}}{{SB}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}.$
Tương tự ta chứng minh được \(\dfrac{{SK}}{{SC}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}\)
$ \Rightarrow HK$//$BD$ suy ra $\dfrac{{SH}}{{SB}} = \dfrac{{HK}}{{BD}} \Leftrightarrow \dfrac{{{x^2}}}{{{x^2} + {a^2}}} = \dfrac{{xa}}{{\sqrt {{x^2} + {a^2}} .a\sqrt 2 }} \Leftrightarrow \dfrac{x}{{\sqrt {{x^2} + {a^2}} }} = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow 2{x^2} = {x^2} + {a^2} \Rightarrow x = a.$
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
