Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD) và SD=a√5. Gọi M là trung điểm SB.
Đường thẳng CD vuông góc với mặt phẳng
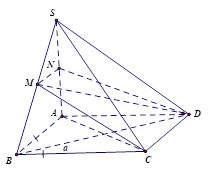
ABCD là hình vuông⇒CD⊥AD (1)
Ta có SA⊥(ABCD)⇒CD⊥SA (2)
Từ ( 1) và (2) suy ra CD⊥(SAD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD) và SD=a√5. Gọi M là trung điểm SB.
Mặt phẳng nào vuông góc với (SAC)?
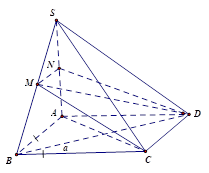
ABCD là hình vuông⇒BD⊥AC (3)
Ta lại có: BD⊥SA (Do SA⊥(ABCD)) (4).
Từ (3) và (4) suy ra BD⊥(SAC), mà BD⊂(SBD) nên (SBD)⊥(SAC)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD) và SD=a√5. Gọi M là trung điểm SB.
Tính góc giữa hai mặt phẳng (MCD) và (ABCD).
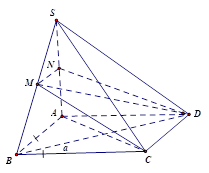
Bước 1:
Kẻ MN∥AB(N∈SA)
Mà AB∥CD
⇒MN∥CD ⇒N∈(MCD)
Bước 2:
{CD⊥AD⊂(SAD)CD⊥ND⊂(SAD)⇒CD⊥(SAD)
Mặt khác,
CD=(MCD)∩(ABCD)
⇒(SAD) vuông góc với (MCD) và (ABCD).
Bước 3:
N∈(MCD)⇒ND⊂(MCD)N∈SA⊂(SAD)⇒ND⊂(SAD)⇒ND=(MCD)∩(SAD)
AD=(ABCD)∩(SAD)
⇒^((MCD),(ABCD))=^(AD,ND)=^NDA=α
Bước 4:
Xét tam giác NDA vuông tại N có: AN=SA2=a, AD=a.
(do SA=√SD2−AD2=√5a2−a2=2a; N là trung điểm SA).
Nên ΔNAD vuông cân tại A ⇒α=45∘.
Vậy góc giữa (MCD) và (ABCD) bằng 45∘
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh a√2, cạnh bên AA′=a (minh họa như hình vẽ). Góc giữa hai mặt phẳng (A′BD) và (C′BD) bằng bao nhiêu độ?
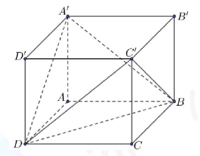
Đáp án
0
Đáp án
0
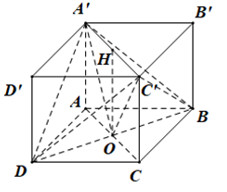
Bước 1: Xác định góc
Vì ABCD là hình vuông nên AC vuông góc BD tại O.
Suy ra BD⊥(A′OC′). Góc giữa hai mặt phẳng (A′BD),(C′BD) là ∠A′OC′
Bước 2: Sử dụng tính chất tam giác vuông cân để tính góc.
Gọi Hlà tâm hình vuông A′B′C′D′ thì H là trung điểm A′C′ và
OH=A′A=aA′H=HC′=A′C′2=A′B′√22=a√2.√22=a
Suy ra các tam giác OHA′;OHC′ vuông cân và ∠A′OC′=90∘
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB=BC=2a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC), SA=√3a. Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
Đáp án
0
Đáp án
0
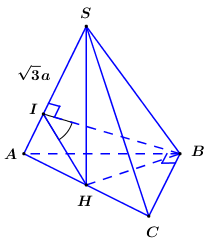
Bước 1: Gọi H là trung điểm của AC, chứng minh SH⊥(SAC),BH⊥(SAC).
Gọi H là trung điểm của AC ta có SH⊥AC (do tam giác SAC cân tại S).
Ta có {(SAC)⊥(ABC)=ACAH⊂(SAC),AH⊥AC ⇒AH⊥(ABC). Tương tự BH⊥(SAC).
Bước 2: Trong (SAB) kẻ BI⊥SA, chứng minh ∠((SAB);(SAC))=∠(BH;HI).
Trong (SAB) kẻ BI⊥SA ta có {SA⊥BISA⊥BH(doBH⊥(SAC))⇒SA⊥(BHI)⇒SA⊥HI
⇒{(SAB)∩(SAC)=SABI⊂(SAB),BI⊥SAHI⊂(SAC),HI⊥SA ⇒∠((SAB);(SAC))=∠(BI;HI).
Bước 3: Sử dụng tính chất tam giác vuông cân, định lí Pytago, hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Vì BH⊥(SAC)(cmt)⇒BH⊥HI ⇒ΔBHI vuông tại I.
Do đó ∠((SAB);(SAC))=∠(BH;HI)=∠BHI.
Tam giác ABC vuông cân tại B có AB=BC=2a nên BH=AB√2=a√2, AC=AB√2=2√2a
Ta có: SH=√SA2−AH2=√3a2−2a2=a.
⇒HI=SH.AHSA=a.√2a√3a=√6a3.
Xét tam giác vuông BHI có tan∠BIH=BHIH=a√2√6a3=√3⇒∠BIH=600
Vậy góc giữa mặt phẳng (SAB) và (SAC) là 600

