Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $C$. Gọi $H$ là trung điểm $AB$. Biết rằng $SH$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và $AB = SH = a.$ Tính cosin của góc $\alpha $ tọa bởi hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: d
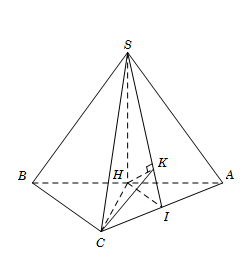
Ta có $SH \bot \left( {ABC} \right) \Rightarrow SH \bot CH$ (1)
Tam giác ABC cân tại C nên $CH \bot AB$ (2)
Từ (1) và (2), suy ra $CH \bot \left( {SAB} \right)$
Gọi I là trung điểm $AC$ $\Rightarrow \,\,HI//BC\xrightarrow{BC\,\bot \,\,AC}HI\bot AC$ (3)
Mặt khác $AC \bot SH$ (do $SH \bot \left( {ABC} \right)$) (4)
Từ (3) và (4), suy ra $AC \bot \left( {SHI} \right)$
Kẻ $HK \bot SI{\rm{ }}\,\left( {K \in SI} \right)$ (5)
Từ $AC \bot \left( {SHI} \right) \Rightarrow AC \bot HK$ (6)
Từ (5) và (6), suy ra $HK \bot \left( {SAC} \right)$
Vì $\left\{ \begin{array}{l}HK \bot \left( {SAC} \right)\\HC \bot \left( {SAB} \right)\end{array} \right.$ nên góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SAB} \right)$ bằng góc giữa hai đường thẳng $HK$ và $HC$
Ta có \(HK \bot \left( {SAC} \right) \Rightarrow HK \bot CK \Rightarrow \Delta CHK\) vuông tại $K.$
Do đó góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SAB} \right)$ là \(\widehat {CHK}\)
Có $CH = \dfrac{1}{2}AB = \dfrac{a}{2}$; $\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{1}{2}.\dfrac{a}{{\sqrt 2 }}} \right)}^2}}} \Rightarrow HK = \dfrac{a}{3}$
Do đó $\cos \widehat {CHK} = \dfrac{{HK}}{{CH}} = \dfrac{{\dfrac{a}{3}}}{{\dfrac{a}{2}}} = \dfrac{2}{3}.$
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
