Câu hỏi:
2 năm trước
Cho hai tam giác $ACD$ và $BCD$ nằm trên hai mặt phẳng vuông góc với nhau và $AC = AD = BC = BD = a,\,\,\,CD = 2x.$ Với giá trị nào của $x$ thì hai mặt phẳng $\left( {ABC} \right)$ và $\left( {ABD} \right)$ vuông góc.
Trả lời bởi giáo viên
Đáp án đúng: a
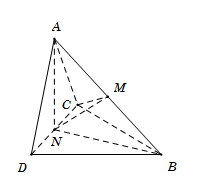
Gọi $M, N$ lần lượt là trung điểm của $AB, CD.$
Ta có $AN \bot CD$ mà $\left( {ACD} \right) \bot \left( {BCD} \right)$
$ \Rightarrow AN \bot \left( {BCD} \right) \Rightarrow AN \bot BN \Rightarrow \Delta ANB$ vuông tại N \( \Rightarrow NM = \dfrac{{AB}}{2}\,\,\left( 1 \right)\)
Tam giác $ABC$ cân tại $C,$ có $M$ là trung điểm của $AB$ $ \Rightarrow CM \bot AB.$
Giả sử $\left( {ABC} \right) \bot \left( {ABD} \right)$ mà $CM \bot AB$$ \Rightarrow CM \bot \left( {ABD} \right) \Rightarrow CM \bot DM.$
Khi đó, $\Delta \,MCD$ vuông tại $M$. Ta có \(\Delta ABC = \Delta ABD\,\,\left( {c.c.c} \right) \Rightarrow CM = DM \Rightarrow \Delta MCD\) vuông cân tại M.
$ \Rightarrow \,\,MN = \dfrac{{CD}}{2}\,\,\,\left( 2 \right)$.
Từ (1) và (2) $ \Rightarrow AB = CD = 2x$
Lại có $\Delta ACD = \Delta BCD\,\,\left( {c.c.c} \right) \Rightarrow AN = BN = \sqrt {A{C^2} - C{N^2}} = \sqrt {{a^2} - {x^2}} ,$ mà $A{B^2} = A{N^2} + B{N^2}.$
Suy ra $2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2} \Leftrightarrow x = \dfrac{{a\sqrt 3 }}{3}.$
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
