Hàm số liên tục

Xét hàm số $f\left( x \right) = {x^3} - 3{x^2} + \left( {2m - 2} \right)x + m - 3$ liên tục trên $\mathbb{R}$.

Giả sử phương trình có ba nghiệm phân biệt ${x_1},{\rm{ }}{x_2},{\rm{ }}{x_3}$ sao cho ${x_1} < - 1 < {x_2} < {x_3}$. Khi đó $f\left( x \right) = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)$.

Ta có $f\left( { - 1} \right) = \left( { - 1 - {x_1}} \right)\left( { - 1 - {x_2}} \right)\left( { - 1 - {x_3}} \right) > 0$ (do ${x_1} <  - 1 < {x_2} < {x_3}$).

Mà $f\left( { - 1} \right) =  - m - 5$ nên suy ra $ - m - 5 > 0 \Leftrightarrow m <  - 5.$

Thử lại: Với $m < - 5$, ta có

$\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) =  - \infty $ nên tồn tại \(a <  - 1\) sao cho $f\left( a \right) < 0$.      \(\left( 1 \right)\)

Do $m <  - 5$ nên $f\left( { - 1} \right) =  - m - 5 > 0$.  \(\left( 2 \right)\)

$f\left( 0 \right) = m - 3 < 0$.          \(\left( 3 \right)\)

$\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) =  + \infty $ nên tồn tại \(b > 0\) sao cho $f\left( b \right) > 0$.         \(\left( 4 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra phương trình có nghiệm thuộc khoảng \(\left( { - \infty ; - 1} \right)\); Từ \(\left( 2 \right)\) và \(\left( 3 \right)\), suy ra phương trình có nghiệm thuộc khoảng \(\left( { - 1;0} \right)\); Từ \(\left( 3 \right)\) và \(\left( 4 \right)\), suy ra phương trình có nghiệm thuộc khoảng \(\left( {0; + \infty } \right).\)

Vậy khi $m <  - 5$ thỏa mãn \(m \in \mathbb{Z},m \in \left( { - 10;10} \right)\) \( \Rightarrow m \in \left\{ { - 9; - 8; - 7; - 6} \right\}.\)

Ta có:

$\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {ax + 1} \sqrt[3]{{bx + 1}} - 1}}{x} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {\sqrt {ax + 1}  - 1} \right)\left( {\sqrt[3]{{bx + 1}} - 1} \right) + \left( {\sqrt {ax + 1}  - 1} \right) + \left( {\sqrt[3]{{bx + 1}} - 1} \right)}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{\dfrac{{ax + 1 - 1}}{{\sqrt {ax + 1}  + 1}}.\dfrac{{bx + 1 - 1}}{{{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1}} + \dfrac{{ax + 1 - 1}}{{\sqrt {ax + 1}  + 1}} + \dfrac{{bx + 1 - 1}}{{{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1}}}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \left[ {\dfrac{{abx}}{{\left( {\sqrt {ax + 1}  + 1} \right)\left( {{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1} \right)}} + \dfrac{a}{{\sqrt {ax + 1}  + 1}} + \dfrac{b}{{{{\sqrt[3]{{bx + 1}}}^2} + \sqrt[3]{{bx + 1}} + 1}}} \right]\\ = 0 + \dfrac{a}{2} + \dfrac{b}{3} = \dfrac{a}{2} + \dfrac{b}{3}\end{array}$

Để hàm số liên tục tại \(x = 0 \) thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow \dfrac{a}{2} + \dfrac{b}{3} = a + b \Leftrightarrow \dfrac{a}{2} + \dfrac{{2b}}{3} = 0 \Leftrightarrow 3a + 4b = 0\)

TXĐ: $D = \mathbb{R}$.

Hàm số $f\left( x \right) = {x^3} - 1000{x^2} + 0,01$ liên tục trên $\mathbb{R}$ nên liên tục trên $\left[ { - 1;0} \right]$, $\left[ {0;1} \right]$, $\left[ {1;2} \right]$ và \(\left[ {2;1000} \right]\) $\left( 1 \right)$.

Ta có $f\left( { - 1} \right) =  - 1000,99$; $f\left( 0 \right) = 0,01$ suy ra $f\left( { - 1} \right).f\left( 0 \right) < 0$, $\left( 2 \right)$.

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm trên khoảng $\left( { - 1;0} \right)$.

Ta có $f\left( 0 \right) = 0,01$; $f\left( 1 \right) =  - 999,99$ suy ra $f\left( 0 \right).f\left( 1 \right) < 0$, $\left( 3 \right)$.

Từ $\left( 1 \right)$ và $\left( 3 \right)$ suy ra phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm trên khoảng $\left( {0;1} \right)$.

Ta có $f\left( 1 \right) =  - 999,99$; $f\left( 2 \right) =  - 39991,99$suy ra $f\left( 1 \right).f\left( 2 \right) > 0$, $\left( 4 \right)$.

Từ $\left( 1 \right)$ và $\left( 4 \right)$ ta chưa thể kết luận về nghiệm của phương trình $f\left( x \right) = 0$ trên khoảng $\left( {1;2} \right)$.

Ta có: $f\left( 2 \right) =  - 39991,99 < 0,$\(f\left( {1000} \right) = 0,01 > 0\) nên phương trình $f\left( x \right) = 0$ có ít nhất \(1\) nghiệm thuộc khoảng \(\left( {2;1000} \right)\)

Mà phương trình bậc ba chỉ có nhiều nhất ba nghiệm nên ở mỗi khoảng I, II, IV thì phương trình đều có \(1\) nghiệm và trên khoảng \(\left( {1;2} \right)\) không có nghiệm.

Bước 1:

\(f(x) = {x^3} - 3{x^2} + 3\)

\(f(0) = 3\)

\(f( - 1) =  - 1\)

\(f(2) =  - 1\)

\(f(3) = 3\)

Bước 2:

\( \Rightarrow f( - 1) \cdot f(0) < 0\)\( \Rightarrow f\left( {{x_1}} \right) = 0,{x_1} \in \left( { - 1;0} \right)\)

\(f(0) \cdot f(2) < 0 \Rightarrow f(z) = 0,{x_2} \in (0;2)\)

\(f(2) \cdot f(3) < 0 \Rightarrow f\left( {{x_3}} \right) = 0,{x_3} \in (2;3)\)

Vậy phương trình  \(f(x) = 0\) có 3 nghiệm phân biệt.

Bước 1:

Ta có: \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \dfrac{{{x^2} - 2x - 3}}{{x - 3}}\) \( = \mathop {\lim }\limits_{x \to 3} \dfrac{{\left( {x + 1} \right)\left( {x - 3} \right)}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \left( {x + 1} \right)\)\( = 4\)

Bước 2:

\(f\left( 3 \right) = 12 - 2m\).

Bước 3:

Để hàm số liên tục trên \(\mathbb{R} \Rightarrow \) Hàm số liên tục tại \(x = 3 \Leftrightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)\)

\( \Leftrightarrow 12 - 2m = 4 \Leftrightarrow 2m = 8\)\( \Leftrightarrow m = 4\).

Bước 1:

\(\begin{array}{l}f( - 2) = m\\\mathop {\lim }\limits_{x \to  - 2} f(x)\\ = \mathop {\lim }\limits_{x \to  - 2} \dfrac{{{x^2} - 4}}{{x + 2}} = \mathop {\lim }\limits_{x \to  - 2} (x - 2) =  - 4\end{array}\)

Bước 2:

Hàm số liên tục tại -2 \( \Leftrightarrow f( - 2) = \mathop {\lim }\limits_{x \to  - 2} f(x)\)\( \Leftrightarrow m =  - 4\)

\(y = {x^2} - 3x + 56\) là hàm đa thức nên liên tục trên \(\mathbb{R}\).

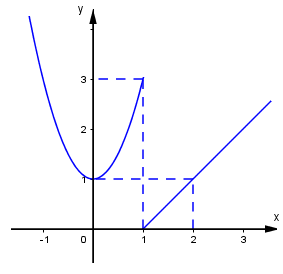
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 3;\,\,\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 0 \) \(\Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to {1^{}}} f\left( x \right)\). Do đó hàm số gián đoạn tại điểm $x = 1.$

TXĐ: \(D = R\backslash \left\{ { - 3; - 2} \right\} = \left( { - \infty ; - 3} \right) \cup \left( { - 3; - 2} \right) \cup \left( { - 2; + \infty } \right)\) nên theo định lí 1, hàm số liên tục trên các khoảng \(\left( { - \infty ; - 3} \right);\,\,\left( { - 3; - 2} \right);\,\,\left( { - 2; + \infty } \right)\) . Vì \(\left( {2;3} \right) \subset \left( { - 2; + \infty } \right) \Rightarrow \) Hàm số liên tục trên \(\left( {2;3} \right)\).

Hàm phân thức \(y = \dfrac{{{x^4} + x}}{{{x^2} + x}}\) có txđ \(D = R\backslash \left\{ {0; - 1} \right\}\) và liên tục trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {0; + \infty } \right)\).

Ta chỉ cần xét tính liên tục của \(y = f\left( x \right)\) tại các điểm \(x = 0;x =  - 1\).

Ta có:

\(\mathop {\lim }\limits_{x \to  - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to  - 1} \dfrac{{{x^4} + x}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to  - 1} \dfrac{{{x^3} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to  - 1} \left( {{x^2} - x + 1} \right) = 3 = f\left( { - 1} \right) \Rightarrow \) Hàm số liên tục tại \(x =  - 1\)

\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^4} + x}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^3} + 1}}{{x + 1}} = 1 = f\left( 0 \right) \Rightarrow \) Hàm số liên tục tại $x = 0.$

Vậy hàm số liên tục tại mọi điểm \(x \in R\).

Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ;0} \right),\left( {0;1} \right),\left( {1; + \infty } \right)\) nên ta chỉ xét tính liên tục của \(y = f\left( x \right)\) tại các điểm \(x = 0,x = 1\).

\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{x^2}}}{{1 + x}} = 0\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\cos x} \right) = 0\\f\left( 0 \right) = \dfrac{0}{{1 + 0}} = 0\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \) \(\Rightarrow \) hàm số liên tục tại $x = 0.$

\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} {x^3} = 1\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{{x^2}}}{{1 + x}} = \dfrac{1}{{1 + 1}} = \dfrac{1}{2}\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) \Rightarrow \)Không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) \( \Rightarrow \) hàm số không liên tục tại $x = 1.$

Vậy hàm số liên tục tại mọi điểm trừ $x = 1.$

Ta có: \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \dfrac{{3 - x}}{{\sqrt {x + 1}  - 2}} = \mathop {\lim }\limits_{x \to 3} \dfrac{{\left( {3 - x} \right)\left( {\sqrt {x + 1}  + 2} \right)}}{{x + 1 - 4}} = \mathop {\lim }\limits_{x \to 3} \left( { - \sqrt {x + 1}  - 2} \right) =  - 4\)

Để hàm số liên tục tại $x = 3$ thì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) \Leftrightarrow m =  - 4\)

$\begin{array}{l}\mathop {\lim }\limits_{x \to {8^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {8^ + }} \dfrac{{x - 8}}{{\sqrt[3]{x} - 2}} = \mathop {\lim }\limits_{x \to {8^ + }} \left( {{{\sqrt[3]{x}}^2} + 2\sqrt[3]{x} + 4} \right)\\ = {2^2} + 2.2 + 4 = 12\\\mathop {\lim }\limits_{x \to {8^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {8^ - }} \left( {ax + 4} \right) = 8a + 4\\f\left( 8 \right) = 8a + 4\end{array}$

Hàm số liên tục tại $x = 8$ \( \Leftrightarrow 12 = 8a + 4 \Leftrightarrow a = 1\)

Ta có \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin 5x}}{{5x}} = 1;\,\,f\left( 0 \right) = a + 2\)

Vậy để hàm số liên tục tại $x = 0$ thì \(a + 2 = 1 \Leftrightarrow a =  - 1\) 

\(f\left( x \right) = \left\{ \begin{array}{l}\cos \dfrac{{\pi x}}{2}\,\,\,\,khi\,\,\left| x \right| \le 1\\\left| {x - 1} \right|\,\,\,\,\,\,\,khi\,\,\left| x \right| > 1\end{array} \right. \Leftrightarrow f\left( x \right) = \left\{ \begin{array}{l}\cos \dfrac{{\pi x}}{2}\,\,\,\,khi\,\, - 1 \le x \le 1\\\left| {x - 1} \right|\,\,\,\,\,\,\,khi\,\,\left[ \begin{array}{l}x > 1\\x <  - 1\end{array} \right.\end{array} \right.\)

Ta có:

$\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left| {x - 1} \right| = 0\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \cos \dfrac{{\pi x}}{2} = \cos \dfrac{\pi }{2} = 0\\f\left( 1 \right) = \cos \dfrac{\pi }{2} = 0\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right) = 0 \Rightarrow $ Hàm số liên tục tại $x = 1.$

$\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \cos \dfrac{{\pi x}}{2} = \cos \dfrac{{ - \pi }}{2} = 0\\\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \left| {x - 1} \right| = 2\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} f\left( x \right) \Rightarrow $Hàm số không liên tục tại \(x =  - 1\).

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt[3]{{2x + 8}} - 2}}{{\sqrt {3x + 4}  - 2}} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {2x + 8 - 8} \right)\left( {\sqrt {3x + 4}  + 2} \right)}}{{\left( {{{\sqrt[3]{{2x + 8}}}^2} + 2\sqrt[3]{{2x + 8}} + 4} \right)\left( {3x + 4 - 4} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{2\left( {\sqrt {3x + 4}  + 2} \right)}}{{3\left( {{{\sqrt[3]{{2x + 8}}}^2} + 2\sqrt[3]{{2x + 8}} + 4} \right)}} \\= \dfrac{{2.\left( {2 + 2} \right)}}{{3\left( {{2^2} + 2.2 + 4} \right)}} = \dfrac{2}{9}\end{array}\)

Hàm số liên tục tại điểm \(x = 0\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow f\left( 0 \right) = \dfrac{2}{9}\)

Hàm số liên tục trên \(\left( {0;9} \right) \cup \left( {9; + \infty } \right)\), ta cần xét tính liên tục của hàm số tại $x = 0$ và $x = 9.$

$\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{3 - \sqrt {9 - x} }}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{9 - \left( {9 - x} \right)}}{{x\left( {3 + \sqrt {9 - x} } \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{1}{{3 + \sqrt {9 - x} }} = \dfrac{1}{6}$

Mà $f\left( 0 \right) = m$ $\Rightarrow $ để hàm số liên tục tại $x = 0$ thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow \dfrac{1}{6} = m\).

$\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {9^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {9^ + }} \dfrac{3}{x} = \dfrac{1}{3}\\\mathop {\lim }\limits_{x \to {9^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {9^ - }} \dfrac{{3 - \sqrt {9 - x} }}{x} = \dfrac{{3 - 0}}{9} = \dfrac{1}{3}\\f\left( 9 \right) = \dfrac{3}{9} = \dfrac{1}{3}\end{array} \right\} $

$ \Rightarrow \mathop {\lim }\limits_{x \to {9^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {9^ - }} f\left( x \right) = f\left( 9 \right) $ $\Rightarrow $ hàm số liên tục tại $x = 9.$

Vậy với \(m = \dfrac{1}{6}\) thì hàm số liên tục trên \(\left[ {0; + \infty } \right)\)

\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\tan x}}{x} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x}.\dfrac{1}{{\cos x}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x}.\mathop {\lim }\limits_{x \to 0} \dfrac{1}{{\cos x}} = 1.\dfrac{1}{1} = 1\\f\left( 0 \right) = 0\end{array} \right\} \\ \Rightarrow \mathop {\lim }\limits_{x \to 0} f\left( x \right) \ne f\left( 0 \right)\)

\( \Rightarrow \) hàm số gián đoạn tại điểm $x = 0,$ do đó loại các đáp án B, C, D.

TXĐ: D = R. Hàm số \(f\left( x \right) = 2{x^4} - 5{x^2} + x + 1\) liên tục trên R.

Ta có: $f\left( { - 1} \right) =  - 3,\,\,f\left( 0 \right) = 1 \Rightarrow f\left( { - 1} \right)f\left( 0 \right) < 0 \Rightarrow $ Phương trình (1) có ít nhất một nghiệm trong \(\left( { - 1;0} \right) \subset \left( { - 2;1} \right)\)

Ta có \(f\left( 0 \right) = 1;f\left( 1 \right) =  - 1 \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0 \Rightarrow \) Phương trình (1) có ít nhất 1 nghiệm thuộc $\left( {0;1} \right) \subset \left( { - 2;1} \right)$

\( \Rightarrow \)  Phương trình (1) có ít nhất hai nghiệm trong \(\left( { - 2;1} \right) \Rightarrow \) Đáp án A sai.

Ta có: $f\left( { - 1} \right) =  - 3,\,\,f\left( 0 \right) = 1 \Rightarrow f\left( { - 1} \right)f\left( 0 \right) < 0 \Rightarrow $ Phương trình (1) có ít nhất một nghiệm trong \(\left( { - 1;0} \right) \subset \left( { - 2;0} \right) \Rightarrow \)Đáp án C sai.

 Ta có \(f\left( 0 \right) = 1;f\left( 1 \right) =  - 1 \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0 \Rightarrow \) Phương trình (1) có ít nhất 1 nghiệm thuộc $\left( {0;1} \right) \subset \left( { - 1;1} \right) \Rightarrow $ Đáp án D sai.

Hàm số đã cho xác định trên R.

Ta có

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{\left| {x - 3} \right|}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{ - \left( {x - 3} \right)}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( { - 1} \right) =  - 1\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\sqrt {{{\left( {x - 3} \right)}^2}} }}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{\left| {x - 3} \right|}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{x - 3}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ + }} \left( 1 \right) = 1\end{array}\)

Vậy $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) \Rightarrow $ Không tồn tại $\mathop {\lim }\limits_{x \to 3} f\left( x \right)$.

Vậy không có giá trị nào của $m$ để hàm số liên tục tại $x = 3.$