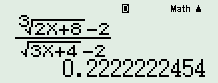Câu hỏi:
2 năm trước
Chọn giá trị của \(f\left( 0 \right)\) đề hàm số $f\left( x \right)=\left\{ \begin{array}{l}
\dfrac{{\sqrt[3]{{2x + 8}} - 2}}{{\sqrt {3x + 4} - 2}}\,khi\,x \ne 0\\
m\,\,\,\,\,khi\,\,\,\,\,x = 0
\end{array} \right.$ liên tục tại điểm $x = 0.$
Trả lời bởi giáo viên
Đáp án đúng: c
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt[3]{{2x + 8}} - 2}}{{\sqrt {3x + 4} - 2}} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {2x + 8 - 8} \right)\left( {\sqrt {3x + 4} + 2} \right)}}{{\left( {{{\sqrt[3]{{2x + 8}}}^2} + 2\sqrt[3]{{2x + 8}} + 4} \right)\left( {3x + 4 - 4} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{2\left( {\sqrt {3x + 4} + 2} \right)}}{{3\left( {{{\sqrt[3]{{2x + 8}}}^2} + 2\sqrt[3]{{2x + 8}} + 4} \right)}} \\= \dfrac{{2.\left( {2 + 2} \right)}}{{3\left( {{2^2} + 2.2 + 4} \right)}} = \dfrac{2}{9}\end{array}\)
Hàm số liên tục tại điểm \(x = 0\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow f\left( 0 \right) = \dfrac{2}{9}\)
Hướng dẫn giải:
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = 0\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\)
Giải thích thêm:
Học sinh có thể sử dụng MTCT để tính \(\mathop {\lim }\limits_{x \to 0} f\left( x \right)\) bằng cách nhập hàm số \(f\left( x \right) = \dfrac{{\sqrt[3]{{2x + 8}} - 2}}{{\sqrt {3x + 4} - 2}}\) vào MTCT, sử dụng phím [CALC], chọn $x = 0,00001$, ta được \( f(x)\approx \dfrac{2}{9}\).
