Chọn khẳng định sai.
+ Vì \(AD\) là tia phân giác \(\widehat {BAC} \Rightarrow D\) là điểm chính giữa cung \(BC\) .
Nên \(OD \bot BC\) \( \Rightarrow \) phương án D đúng
+ Mà \(DE \bot OD\) (\(DE\) là tiếp tuyến của \(\left( O \right)\)) suy ra \(BC{\rm{//}}DE\) \( \Rightarrow \) phương án A đúng.
+) Xét \(\left( O \right)\) có \(\widehat {DAC} = \widehat {DCI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung \(DC\) )
Mà \(\widehat {BAD} = \widehat {DAC}\) ($AD$ là phân giác) nên \(\widehat {KAI} = \widehat {KCI}\) nên tứ giác \(KICA\) nội tiếp \( \Rightarrow \) phương án B đúng.
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
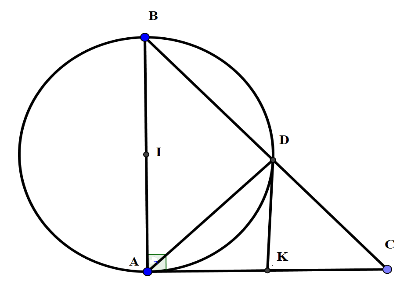
+ Xét đường tròn \(\left( I \right)\) đường kính \(AB\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên $AD \bot BC \Rightarrow $ phương án B đúng.
+) Gọi \(K\) là trung điểm của \(AC \Rightarrow KA = KC = KD \Rightarrow K\) đường tròn đường kính \(AC \Rightarrow \) phương án C đúng.
+) Ta có \(\Delta IBD\) cân tại \(I\) có \(\widehat B = 60^\circ \Rightarrow \Delta IBD\) đều nên \(\widehat {BID} = 60^\circ \)
Độ dài cung nhỏ \(BD\) của \(\left( I \right)\) là $l = \dfrac{{\pi .\dfrac{5}{2}.60}}{{180^\circ }} = \dfrac{{5\pi }}{6}\,\left( {cm} \right) \Rightarrow $ phương án D đúng.
Cho tam giác $ABC$ có \(AB = AC = 3\,\,cm,\,\,\widehat {\rm{A}} = {120^o}.\)Tính độ dài đường tròn ngoại tiếp tam giác $ABC$ .
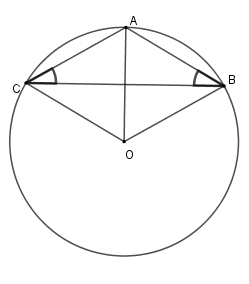
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) . Vì tam giác \(ABC\) cân tại \(A\) nên \(AO\) vừa là đường cao vừa là phân giác của \(\widehat {BAC}\)
Suy ra \(\widehat {CAO} = \dfrac{{120^\circ }}{2} = 60^\circ \) . Xét tam giác \(CAO\) có \(OA = OC;\widehat {CAO} = 60^\circ \Rightarrow \Delta CAO\) đều nên \(OA = OC = AC = 3\,cm\) .
Nên bán kính đường tròn ngoại tiếp \(\Delta ABC\) là \(R = 3\,cm\)
Chu vi đường tròn \(\left( O \right)\) là \(C = 2\pi R = 6\pi \,\,\left( {cm} \right)\)
Chu vi đường tròn ngoại tiếp tam giác đều cạnh \(a\,\left( {cm} \right)\) là
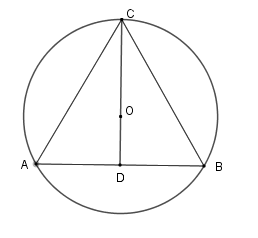
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác đều \(BAC\) , suy ra \(O\) cũng là trọng tâm của tam giác \(ABC\) .
Tia \(CO \bot AB\) tại \(D\) thì $D$ là trung điểm của \(AB\) \( \Rightarrow OC = \dfrac{2}{3}CD\)
Xét tam giác vuông \(ADC\) có \(AC = a\,;\,\widehat {CAD} = 60^\circ \Rightarrow CD = AC.\sin 60^\circ = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow OC = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Nên bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = \dfrac{{a\sqrt 3 }}{3} \Rightarrow C = 2\pi R = \dfrac{{2\pi a\sqrt 3 }}{3}\) .
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây\(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(4\pi \,(cm).\) Độ dài cung lớn \(BC\) là
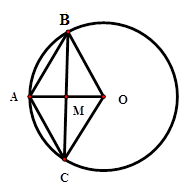
Vì độ dài đường tròn là \(4\pi \) nên $4\pi = 2\pi .R \Rightarrow R = 2\,cm$ (\(R\) là bán kính đường tròn)
Xét tứ giác \(ABOC\) có hai đường chéo \(AO \bot BC\) tại \(M\) là trung điểm mỗi đường nên tứ giác \(ABOC\) là hình thoi.
Suy ra \(OB = OC = AB \Rightarrow \Delta ABO\) đều \( \Rightarrow \widehat {AOB} = 60^\circ \Rightarrow \widehat {BOC} = 120^\circ \)
Suy ra số đo cung lớn \(BC\) là \(360^\circ - 120^\circ = 240^\circ \)
Độ dài cung lớn \(BC\) là \(l = \dfrac{{\pi .2.240}}{{180}} = \dfrac{{8\pi }}{3}\,\left( {cm} \right).\)
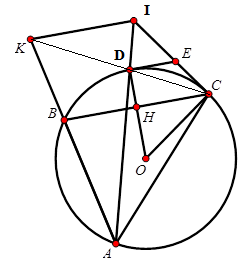
Cho đường tròn $(O; R)$ với dây cung $BC$ cố định. Điểm $A$ thuộc cung lớn $BC$. Đường phân giác của góc \(\widehat {BAC}\) cắt đường tròn $(O$) tại $D$. Các tiếp tuyến của đường tròn $(O; R)$ tại $C$ và $D$ cắt nhau tại $E$. Tia $CD$ cắt $AB$ tại $K$, đường thẳng $AD$ cắt $CE$ tại $I.$
Chọn khẳng định sai.

+ Vì \(AD\) là tia phân giác \(\widehat {BAC} \Rightarrow D\) là điểm chính giữa cung \(BC\) .
Nên \(OD \bot BC\) \( \Rightarrow \) phương án D đúng
+ Mà \(DE \bot OD\) (\(DE\) là tiếp tuyến của \(\left( O \right)\)) suy ra \(BC{\rm{//}}DE\) \( \Rightarrow \) phương án A đúng.
+) Xét \(\left( O \right)\) có \(\widehat {DAC} = \widehat {DCI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung \(DC\) )
Mà \(\widehat {BAD} = \widehat {DAC}\) ($AD$ là phân giác) nên \(\widehat {KAI} = \widehat {KCI}\) nên tứ giác \(KICA\) nội tiếp \( \Rightarrow \) phương án B đúng.
Cho đường tròn $(O; R)$ với dây cung $BC$ cố định. Điểm $A$ thuộc cung lớn $BC$. Đường phân giác của góc \(\widehat {BAC}\) cắt đường tròn $(O$) tại $D$. Các tiếp tuyến của đường tròn $(O; R)$ tại $C$ và $D$ cắt nhau tại $E$. Tia $CD$ cắt $AB$ tại $K$, đường thẳng $AD$ cắt $CE$ tại $I.$
Cho \(BC = R\sqrt 3 .\)Tính theo $R$ độ dài cung nhỏ $BC$ của đường tròn (O; R).
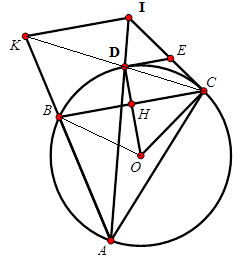
Gọi \(OD \cap BC\) tại \(H\) thì \(H\) là trung điểm \(BC\) (do \(OD \bot BC\) tại \(H\) )\( \Rightarrow HC = \dfrac{{BC}}{2} = \dfrac{{R\sqrt 3 }}{2}\)
Xét tam giác vuông \(HOC\) có \(\sin \widehat {HOC} = \dfrac{{HC}}{{OC}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {HOC} = 60^\circ \Rightarrow \widehat {BOC} = 120^\circ \)
Độ dài cung nhỏ \(BC\) là \(l = \dfrac{{\pi .R.120}}{{180}} = \dfrac{{2\pi R}}{3}\) \(\left( {cm} \right)\) .
Cho tam giác đều ABC nội tiếp đường tròn (O; R). Kẻ đường kính AD cắt BC tại H. Gọi M là một điểm trên cung nhỏ AC. Hạ \(BK \bot AM\) tại K. Đường thẳng BK cắt CM tại E. Tia BE cắt đường tròn (O; R) tại N (N khác B).
Chọn câu đúng. Tam giác MBE
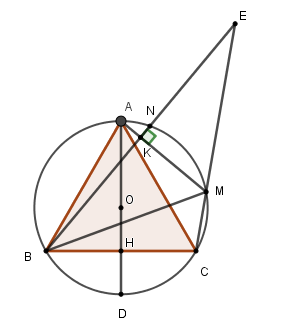
Xét đường tròn \(\left( O \right)\) có tam giác \(ABC\) đều nên sđ \(AB = sd\,AC = sd\,BC = \dfrac{{360^\circ }}{3} = 120^\circ \)
\(\widehat {AMB}\) là góc nội tiếp chắn cung \(AB \Rightarrow \widehat {AMB} = \dfrac{1}{2}sd\,AB = \dfrac{{120^\circ }}{2} = 60^\circ \)
Suy ra \(\widehat {KBM} = 90^\circ - \widehat {KMB} = 90^\circ - 60^\circ = 30^\circ \) suy ra \(sd\,NM = 2.\widehat {NBM} = 2.30^\circ = 60^\circ \)
\(\widehat {NBM} = 30^\circ \left( {cmt} \right)\) và \(\widehat {BEM} = \dfrac{1}{2}\left( {sd\,BC - sd\,NM} \right) = \dfrac{1}{2}\left( {120^\circ - 60^\circ } \right) = 30^\circ \) nên tam giác \(MBE\) cân tại \(M.\)
Cho tam giác đều ABC nội tiếp đường tròn (O; R). Kẻ đường kính AD cắt BC tại H. Gọi M là một điểm trên cung nhỏ AC. Hạ \(BK \bot AM\) tại K. Đường thẳng BK cắt CM tại E. Tia BE cắt đường tròn (O; R) tại N (N khác B).
Tính độ dài cung nhỏ MN theo R.
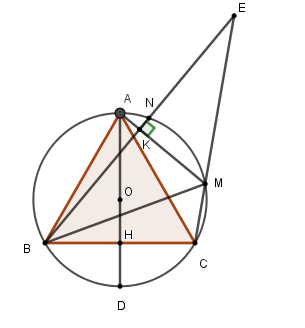
Độ dài cung \(NM\) là \(l = \dfrac{{\pi R.60}}{{180}} = \dfrac{{\pi R}}{3}.\)

