Câu hỏi:
2 năm trước
Cho đường tròn $(O; R)$ với dây cung $BC$ cố định. Điểm $A$ thuộc cung lớn $BC$. Đường phân giác của góc \(\widehat {BAC}\) cắt đường tròn $(O$) tại $D$. Các tiếp tuyến của đường tròn $(O; R)$ tại $C$ và $D$ cắt nhau tại $E$. Tia $CD$ cắt $AB$ tại $K$, đường thẳng $AD$ cắt $CE$ tại $I.$
Chọn khẳng định sai.
Trả lời bởi giáo viên
Đáp án đúng: c
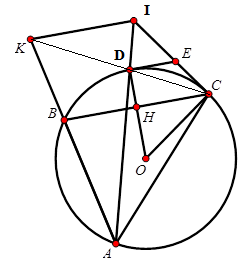
+ Vì \(AD\) là tia phân giác \(\widehat {BAC} \Rightarrow D\) là điểm chính giữa cung \(BC\) .
Nên \(OD \bot BC\) \( \Rightarrow \) phương án D đúng
+ Mà \(DE \bot OD\) (\(DE\) là tiếp tuyến của \(\left( O \right)\)) suy ra \(BC{\rm{//}}DE\) \( \Rightarrow \) phương án A đúng.
+) Xét \(\left( O \right)\) có \(\widehat {DAC} = \widehat {DCI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung \(DC\) )
Mà \(\widehat {BAD} = \widehat {DAC}\) ($AD$ là phân giác) nên \(\widehat {KAI} = \widehat {KCI}\) nên tứ giác \(KICA\) nội tiếp \( \Rightarrow \) phương án B đúng.
Hướng dẫn giải:
Sử dụng các kiến thức về liên hệ giữa đường kính và dây cung, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung, các dấu hiệu nhận biết tứ giác nội tiếp.
