Trả lời bởi giáo viên
Đáp án đúng: d
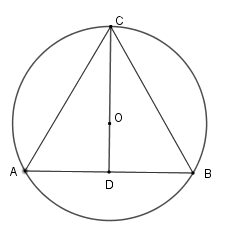
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác đều \(BAC\) , suy ra \(O\) cũng là trọng tâm của tam giác \(ABC\) .
Tia \(CO \bot AB\) tại \(D\) thì $D$ là trung điểm của \(AB\)\( \Rightarrow OC = \dfrac{2}{3}CD\)
Xét tam giác vuông \(ADC\) có \(AC = 3\,;\,\widehat {CAD} = 60^\circ \Rightarrow CD = AC.\sin 60^\circ = \dfrac{{3\sqrt 3 }}{2}\) \( \Rightarrow OC = \dfrac{2}{3}.\dfrac{{3\sqrt 3 }}{2} = \sqrt 3 \) cm
Nên bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = \sqrt 3 \Rightarrow C = 2\pi R = 2\pi \sqrt 3 \left( {cm} \right)\) .
Hướng dẫn giải:
Sử dụng công thức chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\,\)

