Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 4\,cm$ , \(\widehat B = {50^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
Trả lời bởi giáo viên
Đáp án đúng: d
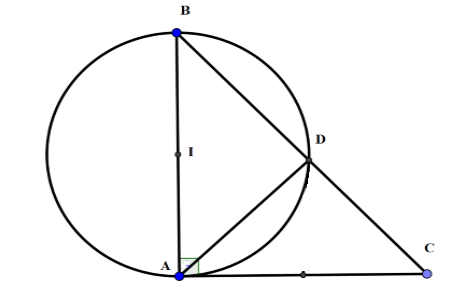
+) Xét tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = 50^\circ \) nên \(\widehat C = 90^\circ - 50^\circ = 40^\circ .\) Do đó A đúng.
+) Vì \(AC \bot AB\) và \(A \in \left( {I;\dfrac{{AB}}{2}} \right)\) nên \(AC\) là tiếp tuyến của \(\left( I \right) \Rightarrow \widehat {DAC} = \widehat B = 50^\circ \) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau) nên C đúng.
+) Vì \(\widehat {DAC} = 50^\circ \Rightarrow \widehat {BAD} = 90^\circ - 50^\circ = 40^\circ \) suy ra số đo cung \(BD\) nhỏ là \(n^\circ = 2.40^\circ = 80^\circ \)
Độ dài cung nhỏ \(BD\) của \(\left( I \right)\) là $l = \dfrac{{\pi .\dfrac{4}{2}.80}}{{180}} = \dfrac{{8\pi }}{9}\,\left( {cm} \right) $ nên phương án B đúng.
+ Số đo cung lớn \(BD\) là \(360^\circ - 80^\circ = 280^\circ \)
Độ dài cung lớn \(BD\) là \({l_1} = \dfrac{{\pi \dfrac{4}{2}.280}}{{180}} = 3\pi \)(cm) nên D sai.
Hướng dẫn giải:
+ Sử dụng tổng hai góc nhọn trong tam giác vuông bằng \(90^\circ .\)
+ Sử dụng: Góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+ Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
