Cho tam giác $ABC$ có \(AB = AC = 4\,\,cm,\,\,\widehat {\rm{A}} = {100^o}.\) Tính độ dài đường tròn ngoại tiếp tam giác $ABC$.

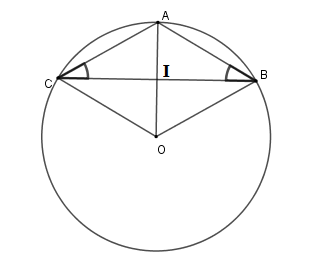
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) . Vì tam giác \(ABC\) cân tại \(A\) nên \(AO\) vừa là đường cao vừa là phân giác của \(\widehat {BAC}\)

Suy ra \(\widehat {CAO} = \dfrac{{100^\circ }}{2} = 50^\circ \) .

Gọi \(I\) là giao điểm của \(AO\) và \(BC\).  Xét tam giác \(CAI\) có \(AC = 4;\,\widehat {CAI} = 50^\circ \) nên  \(\sin \widehat {CAI} = \dfrac{{CI}}{{AC}} \Leftrightarrow CI = AC.\sin \widehat {CAI} = 4.\sin 50^\circ \) (cm).

Xét tam giác \(OAC\) cân tại \(O\) (vì \(OA = OC\)) có \(\widehat {OCA} = \widehat {OAC} = 50^\circ  \Rightarrow \widehat {AOC} = 180^\circ  - 50^\circ  - 50^\circ  = 80^\circ \)

Xét tam giác \(CIO\) vuông tại \(I\) có \(\sin \widehat {COI} = \dfrac{{CI}}{{OC}} \Rightarrow OC = \dfrac{{IC}}{{\sin \widehat {COI}}} = \dfrac{{4\sin 50^\circ }}{{\sin 80^\circ }} \approx 3,11\)

Nên bán kính đường tròn ngoại tiếp \(\Delta ABC\) là \(R \approx 3,11\,cm\)

Chu vi đường tròn \(\left( O \right)\) là $C = 2\pi R \approx 6,22\pi \,\,\left( {cm} \right)$