Câu hỏi:
2 năm trước
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây\(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(4\pi \,(cm).\) Độ dài cung lớn \(BC\) là
Trả lời bởi giáo viên
Đáp án đúng: d
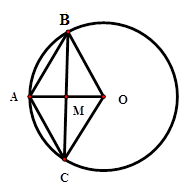
Vì độ dài đường tròn là \(4\pi \) nên $4\pi = 2\pi .R \Rightarrow R = 2\,cm$ (\(R\) là bán kính đường tròn)
Xét tứ giác \(ABOC\) có hai đường chéo \(AO \bot BC\) tại \(M\) là trung điểm mỗi đường nên tứ giác \(ABOC\) là hình thoi.
Suy ra \(OB = OC = AB \Rightarrow \Delta ABO\) đều \( \Rightarrow \widehat {AOB} = 60^\circ \Rightarrow \widehat {BOC} = 120^\circ \)
Suy ra số đo cung lớn \(BC\) là \(360^\circ - 120^\circ = 240^\circ \)
Độ dài cung lớn \(BC\) là \(l = \dfrac{{\pi .2.240}}{{180}} = \dfrac{{8\pi }}{3}\,\left( {cm} \right).\)
Hướng dẫn giải:
Bước 1: Tìm bán kính của đường tròn dựa vào công thức tính chu vi \(C = 2\pi R.\)
Bước 2: Sử dụng công thức tính độ dài cung tròn: \(l = \dfrac{{\pi Rn}}{{180}}.\)
