Cho tam giác đều ABC nội tiếp đường tròn (O; R). Kẻ đường kính AD cắt BC tại H. Gọi M là một điểm trên cung nhỏ AC. Hạ \(BK \bot AM\) tại K. Đường thẳng BK cắt CM tại E. Tia BE cắt đường tròn (O; R) tại N (N khác B).

Tính độ dài cung nhỏ MN theo R.

$70^\circ $

$80^\circ $

$65^\circ $

$85^\circ $

Độ dài nửa đường tròn đường kính $AB$ gấp ba lần độ dài của nửa đường tròn đường kính $AC$

Độ dài nửa đường tròn đường kính $AB$ gấp \(1,5\) lần độ dài của nửa đường tròn đường kính $BC$.

Độ dài nửa đường tròn đường kính $AB$ bằng tổng các độ dài của hai nửa đường tròn đường kính $BC$ và $AC$

Độ dài nửa đường tròn đường kính $BC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AC$ và $AB$

\(\widehat {BCA} = 40^\circ \)

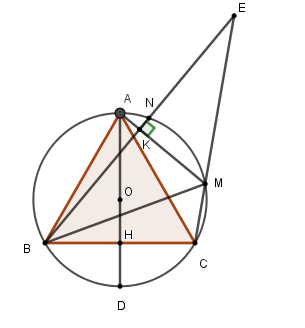
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là $\dfrac{{8\pi }}{9}\,\,\left( {cm} \right)$  

\(\widehat {DAC} = 50^\circ \)

Độ dài cung lớn $BD$ của \(\left( I \right)\) là \(\dfrac{{3\pi }}{2}\,\,\left( {cm} \right)\)

$6,22\pi $

$3,11\pi $

$6\pi $

$12,44\pi $

$\dfrac{{4\pi \sqrt 3 }}{3}\left( {cm} \right)$

$\pi \sqrt 3 \left( {cm} \right)$

$\dfrac{{2\pi \sqrt 3 }}{3}\left( {cm} \right)$

$2\pi \sqrt 3 \left( {cm} \right)$

$\dfrac{{4\pi }}{3}$

$8\pi $

$4\pi $

$2\pi $

\(\pi R\)

\(\dfrac{{\pi R}}{2}\)

\(\dfrac{{\pi R}}{3}\)

\(\dfrac{{\pi R}}{4}\)