Có bao nhiêu giá trị của tham số \(m\) để đường thẳng \(d:y = - \dfrac{3}{2}x + \dfrac{m}{2}\) và parabol \(\left( P \right):y = - \dfrac{1}{2}{x^2}\) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thỏa mãn \(2{x_1} + 3{x_2} = 13\)
Phương trình hoành độ giao điểm \( - \dfrac{1}{2}{x^2} = - \dfrac{3}{2}x + \dfrac{m}{2} \Leftrightarrow {x^2} - 3x + m = 0\) có \(\Delta = 9 - 4m\)
Để đường thẳng \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thì \(\Delta > 0 \Leftrightarrow 9 - 4m > 0 \Leftrightarrow m < \dfrac{9}{4}\)
Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\,\left( 1 \right)\\{x_1}.{x_2} = m\,\left( 2 \right)\end{array} \right.\)
Ta có \(2{x_1} + 3{x_2} = 13\)\( \Leftrightarrow {x_1} = \dfrac{{13 - 3{x_2}}}{2}\) thay vào phương trình \(\left( 1 \right)\) ta được \(\dfrac{{13 - 3{x_2}}}{2} + {x_2} = 3 \Leftrightarrow {x_2} = 7 \Rightarrow {x_1} = - 4\)
Thay \({x_2} = 7;{x_1} = - 4\) vào phương trình \(\left( 2 \right)\) ta được \(7.\left( { - 4} \right) = m \Leftrightarrow m = - 28\) (TM )
Vậy \(m = - 28\) là giá trị cần tìm.
Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm, tìm \(m\) để \({x_2}\left( {x_1^2 - 1} \right) = 3.\)
Gọi \({x_1},\,\,{x_2}\) là các hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) \( \Rightarrow \) \({x_1},\,\,{x_2}\) là các nghiệm của phương trình \(\left( * \right)\)
\( \Rightarrow x_1^2 = m{x_1} + 1\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = - 1\end{array} \right..\)
Theo đề bài ta có: \({x_2}\left( {x_1^2 - 1} \right) = 3\)
\(\begin{array}{l} \Leftrightarrow {x_2}\left( {m{x_1} + 1 - 1} \right) = 3\\ \Leftrightarrow m{x_1}{x_2} = 3\\ \Leftrightarrow - m = 3\\ \Leftrightarrow m = - 3.\end{array}\)
Vậy \(m = - 3\) thỏa mãn bài toán.
Vị trí tương đối của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) là:
Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là: \({x^2} = mx + 1 \Leftrightarrow {x^2} - mx - 1 = 0\,\,\,\left( * \right)\)
Phương trình \(\left( * \right)\) có: \(\Delta = {m^2} + 4 > 0\,\,\forall m\)
\( \Rightarrow \left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m.\)
\( \Rightarrow \left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\)
Tìm \(m\) để đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) cùng đi qua điểm có hoành độ \(x = 2.\)
Gọi \(A\left( {2;\,\,{y_A}} \right)\) là điểm mà đường thẳng \(\left( d \right)\) và parabol \(\left( P \right)\) đều đi qua.
Khi đó ta có: \(A\left( {2;\,{y_A}} \right) \in \left( P \right)\) \( \Rightarrow {y_A} = {2^2} = 4\)\( \Rightarrow A\left( {2;\,\,4} \right).\)
Lại có: \(A\left( {2;\,\,4} \right) \in \left( d \right)\) \( \Rightarrow 4 = m.2 + 1 \Leftrightarrow m = \dfrac{3}{2}\)
Vậy \(m = \dfrac{3}{2}\) thỏa mãn bài toán.
Đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right)$ tiếp xúc với nhau khi phương trình $a{x^2} = mx + n$ có
Đường thẳng $d$ và parabol $\left( P \right)$ tiếp xúc với nhau khi phương trình
$a{x^2} = mx + n \Leftrightarrow a{x^2} - mx - n = 0$ có nghiệm kép $\left( {\Delta = 0} \right)$
Chọn khẳng định đúng. Nếu phương trình $a{x^2} = mx + n$ vô nghiệm thì đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$
Đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$ không cắt nhau khi phương trình $a{x^2} = mx + n$ vô nghiệm.
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
Xét phương trình hoành độ giao điểm ${x^2} = 2x + 4 \Leftrightarrow {x^2} - 2x - 4 = 0$ có $\Delta ' = 5 > 0$ nên phương trình có hai nghiệm phân biệt hay đường thẳng cắt parabol tại hai điểm phân biệt.
Tìm tham số $m$ để đường thẳng $d:y = \dfrac{1}{2}x + m$ tiếp xúc với parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$
Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = \dfrac{1}{2}x + m \Leftrightarrow {x^2} - x - 2m = 0$ có $\Delta = 8m + 1$
Để đường thẳng $d$ tiếp xúc với parabol $\left( P \right)$ thì $\Delta = 0 \Leftrightarrow 8m + 1 = 0 \Leftrightarrow m = - \dfrac{1}{8}$.
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = mx + 2 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4$
Vì $\Delta ' = {m^2} + 4 > 0;\forall m$ nên đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt với mọi $m$.
Tìm tham số $m$ để đường thẳng $d:y = 2x + m$ và parabol $\left( P \right):y = 2{x^2}$ không có điểm chung
Xét phương trình hoành độ giao điểm $2{x^2} = 2x + m \Leftrightarrow 2{x^2} - 2x - m = 0$ có $\Delta ' = 1 + 2m$
Để đường thẳng $d:y = 2x + m$ không cắt parabol $\left( P \right):y = 2{x^2}$ thì $\Delta ' < 0 \Leftrightarrow 2m + 1 < 0 \Leftrightarrow m < - \dfrac{1}{2}$
Tìm tham số $m$ để đường thẳng $d:y = mx + m + 1$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt nằm bên trái trục tung.
Phương trình hoành độ giao điểm ${x^2} = mx + m + 1 \Leftrightarrow {x^2} - mx - m - 1 = 0\left( * \right)$ có
$\Delta = {m^2} - 4\left( { - m - 1} \right) = {m^2} + 4m + 4 = {\left( {m + 2} \right)^2} \ge 0$, $\forall m$; $S = {x_1} + {x_2} = m;P = {x_1}.{x_2} = - m - 1$ với ${x_1};{x_2}$ là hai nghiệm của phương trình (*).
Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm bên trái trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm âm phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S < 0\\P > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 2} \right)^2} > 0\\m < 0\\ - m - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 2\\m < 0\\m < - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < - 1\\m \ne - 2\end{array} \right.$
Vậy $\left\{ \begin{array}{l}m < - 1\\m \ne - 2\end{array} \right.$ .
Tìm tham số $m$ để đường thẳng $d:y = \left( {m - 2} \right)x + 3m$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt nằm hai phía của trục tung.
Phương trình hoành độ giao điểm ${x^2} = \left( {m - 2} \right)x + 3m $
$\Leftrightarrow {x^2} - \left( {m - 2} \right)x - 3m = 0$
Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm hai phía trục tung
$ \Leftrightarrow $ phương trình (*) có hai nghiệm trái dấu
$ \Leftrightarrow ac < 0$
$ \Leftrightarrow - 3m < 0 \Leftrightarrow m > 0$.
Có bao nhiêu giá trị của tham số $m$ để đường thẳng $d:y = 2mx + 4$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn $\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}} = - 3$
Phương trình hoành độ giao điểm ${x^2} = 2mx + 4 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4 > 0;\forall m$
nên đường thẳng $d$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$
Theo hệ thức Vi-et ta có $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = - 4\end{array} \right.$(${x_1};{x_2} \ne 0$)
Ta có $\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}} = - 3$$ \Leftrightarrow \dfrac{{{x_1}^2 + x_2^2}}{{{x_1}{x_2}}} = - 3 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} + {x_1}{x_2} = 0 \Leftrightarrow 4{m^2} - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.$
Vậy $m = 1;m = - 1$ là các giá trị cần tìm.
Có bao nhiêu giá trị nguyên của tham số $m$ để đường thẳng $d:y = 2mx - 2m + 3$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt có tọa độ $\left( {{x_1};{y_1}} \right);\left( {{x_2};{y_2}} \right)$ thỏa mãn ${y_1} + {y_2} < 9$
Phương trình hoành độ giao điểm ${x^2} = 2mx - 2m + 3 \Leftrightarrow {x^2} - 2mx + 2m - 3 = 0$ có $\Delta ' = {m^2} - 2m + 3 = {\left( {m - 1} \right)^2} + 2 > 0;\forall m$
Nên nên đường thẳng $d$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có tọa độ $\left( {{x_1};{y_1}} \right);\left( {{x_2};{y_2}} \right)$
Ta có ${y_1} = x_1^2;{y_2} = x_2^2$.
Theo hệ thức Vi-et: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = 2m - 3\end{array} \right.$
Xét ${y_1} + {y_2} < 9$$ \Leftrightarrow x_1^2 + x_2^2 < 9 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} < 9 \Leftrightarrow 4{m^2} - 4m + 6 - 9 < 0$$ \Leftrightarrow 4{m^2} - 4m - 3 < 0 \Leftrightarrow \left( {2m + 1} \right)\left( {2m - 3} \right) < 0$$ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2m + 1 < 0\\2m - 3 > 0\end{array} \right.\\\left\{ \begin{array}{l}2m + 1 > 0\\2m - 3 < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m < - \dfrac{1}{2}\\m > \dfrac{3}{2}\end{array} \right.\\\left\{ \begin{array}{l}m > - \dfrac{1}{2}\\m < \dfrac{3}{2}\end{array} \right.\end{array} \right. \Rightarrow - \dfrac{1}{2} < m < \dfrac{3}{2}$
Mà $m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1} \right\}$
Vậy có hai giá trị của $m$ thỏa mãn.
Cho đường thẳng \(d\) :\(y = - 3x + 1\) và parabol : \(\left( P \right)\)\(y = m{x^2}\left( {m \ne 0} \right)\). Tìm \(m\) để \(d\) và \(\left( P \right)\) cắt nhau tại hai điểm \(A\) và \(B\) phân biệt và cùng nằm về một phía đối với trục tung.
Phương trình hoành độ giao điểm $m{x^2} = - 3x + 1 \Leftrightarrow m{x^2} + 3x - 1 = 0\,\left( * \right)$ có $\Delta = 9 + 4m$; $P = {x_1}.{x_2} = \dfrac{{ - 1}}{m}$ với ${x_1};{x_2}$ là hai nghiệm của phương trình (*).
Đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm phân biệt nằm cùng một phía với trục tung $ \Leftrightarrow $ phương trình (*) có hai nghiệm phân biệt cùng dấu$ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}4m + 9 > 0\\\dfrac{{ - 1}}{m} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - \dfrac{9}{4}\\m < 0\end{array} \right. \Leftrightarrow - \dfrac{9}{4} < m < 0$
Vậy $ - \dfrac{9}{4} < m < 0$.
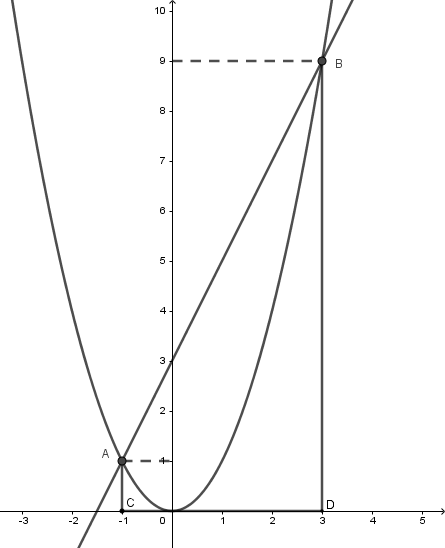
Cho parabol $\left( P \right):y = {x^2}$ và $d:y = 2x + 3.$
Tìm tọa độ giao điểm $A,B$ của $\left( P \right)$ và $ d$.
Phương trình hoành độ giao điểm ${x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \Rightarrow y = {\left( { - 1} \right)^2} = 1\\x = 3 \Rightarrow y = {3^2} = 9\end{array} \right.$
Giao điểm của $d$ và $\left( P \right)$ là $A\left( { - 1;1} \right);B\left( {3;9} \right)$.
Cho parabol $\left( P \right):y = {x^2}$ và $d:y = 2x + 3.$
Với giao điểm $A,B$ của $\left( P \right)$ và $d$ ở câu trước . Gọi $C,D$ lần lượt là hình chiếu vuông góc của $A,B$ lên $Ox$. Tính diện tích tứ giác ${\rm{ABDC}}$.
Ta có $A\left( { - 1;1} \right);B\left( {3;9} \right)$ nên $C\left( { - 1;0} \right);D\left( {3;0} \right)$
$ \Rightarrow AC = \sqrt {{0^2} + {{\left( { - 1} \right)}^2}} = 1;$
$DC = 4;BD = \sqrt {{0^2} + {9^2}} = 9.$
Vì $AC \bot BC;BD \bot BC \Rightarrow ABDC$ là hình thang vuông nên ${S_{ABDC}} = \dfrac{{\left( {AC + BD} \right).DC}}{2} = 20$ (đvdt)
Tìm giá trị của tham số $m$ để đường thẳng $d:y = - \dfrac{1}{2}x + m$ và parabol $\left( P \right):y = - \dfrac{1}{4}{x^2}$ cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn \(3{x_1} + 5{x_2} = 5\)
Phương trình hoành độ giao điểm $ - \dfrac{1}{4}{x^2} = - \dfrac{1}{2}x + m \Leftrightarrow {x^2} - 2x + 4m = 0$ có $\Delta ' = 1 - 4m$
Để đường thẳng $d$ luôn cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thì $\Delta > 0 \Leftrightarrow 1 - 4m > 0 \Leftrightarrow m < \dfrac{1}{4}$
Theo hệ thức Vi-et ta có $\left\{ \begin{array}{l}{x_1} + {x_2} = 2\,\left( 1 \right)\\{x_1}.{x_2} = 4m\,\left( 2 \right)\end{array} \right.$
Ta có \(3{x_1} + 5{x_2} = 5\)$ \Leftrightarrow {x_1} = \dfrac{{5 - 5{x_2}}}{3}$ thay vào phương trình $\left( 1 \right)$ ta được $\dfrac{{5 - 5{x_2}}}{3} + {x_2} = 2 \Leftrightarrow {x_2} = - \dfrac{1}{2} \Rightarrow {x_1} = \dfrac{5}{2}$
Thay ${x_2} = - \dfrac{1}{2};{x_1} = \dfrac{5}{2}$ vào phương trình $\left( 2 \right)$ ta được $\left( { - \dfrac{1}{2}} \right).\dfrac{5}{2} = 4m \Leftrightarrow m = - \dfrac{5}{{16}}$ (TM )
Vậy $m = - \dfrac{5}{{16}}$ là giá trị cần tìm.
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(d:y = \left( {{m^2} + 2} \right)x - {m^2}\). Tìm \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về bên phải trục tung.
Xét phương trình hoành độ giao điểm \({x^2} = \left( {{m^2} + 2} \right)x - {m^2} \Leftrightarrow {x^2} - \left( {{m^2} + 2} \right)x + {m^2} = 0\left( 1 \right)\).
\(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về bên phải trục tung khi và chỉ khi phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt cùng dương
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\Delta = {\left( {{m^2} + 2} \right)^2} - 4{m^2} > 0\\S = {m^2} + 2 > 0\\P = {m^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {{m^2} - 2m + 2} \right)\left( {{m^2} + 2m + 2} \right) > 0\\m \ne 0\end{array} \right.\)
Mà \({m^2} - 2m + 2 = {\left( {m - 1} \right)^2} + 1 > 0\,\,\forall m;\)\({m^2} + 2m + 2 = {\left( {m + 1} \right)^2} + 1 > 0\,\,\forall m\) nên \(\left( {{m^2} - 2m + 2} \right)\left( {{m^2} + 2m + 2} \right) > 0;\,\forall m\)
Từ đó \(m \ne 0\) thỏa mãn đề bài.
Cho parabol \(\left( P \right)\) có đỉnh \(O\) và đi qua điểm \(A\left( {2;4} \right)\) và đường thẳng \(\left( d \right):y = 2(m - 1)x + 2m + 2\) (với \(m\) là tham số). Giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt là
Parabol \(\left( P \right)\) có đỉnh \(O\) nên có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
Mà \(\left( P \right)\) đi qua điểm \(A\left( {2;4} \right)\) nên toạ độ \(A\) thoả mãn phương trình parabol \(\left( P \right)\) suy ra \(4 = a{.2^2} = 4a \Leftrightarrow a = 1\) (thoả mãn \(a \ne 0\))
Phương trình parabol \(\left( P \right)\) là \(y = {x^2}\).
\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt.
Suy ra phương trình \({x^2} - 2(m - 1)x - 2m - 2 = 0\) có hai nghiệm phân biệt.
\( \Leftrightarrow \Delta ' = {( - (m - 1))^2} + 2m + 2 > 0\)\( \Leftrightarrow {m^2} - 2m + 1 + 2m + 2 > 0\)\( \Leftrightarrow {m^2} + 3 > 0\) (luôn đúng)
Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.

