Lớp \(11\;{\rm{A}}2\) có 45 bạn học sinh. Đầu năm cô giáo muốn chọn ra một ban cô sự lớp từ 45 bạn học sinh lớp 11A2 gồm một lớp trưởng, một lớp phó học tập, một lớp phó văn thể mĩ, hai thư kí. Số cách cô giáo chọn ra một ban cán sự lớp như vậy là
Bước 1. Chọn 3 bạn trong đó có một lớp trưởng, một lớp phó học tập, một lớp phó văn thể mĩ từ 45 bạn. Sau đó chọn 2 bạn làm thư kí từ 42 bạn còn lại.
Để chọn ra ban cán sự lớp thỏa mãn yêu cầu, ta tiến hành chọn theo hai bước sau:
+) Chọn 3 bạn trong đó có một lớp trưởng, một lớp phó học tập, một lớp phó văn thể mĩ từ 45 bạn. Mỗi một cách chọn ra một ban cán sự lớp gồm ba bạn trong đó có một lớp trưởng, một lớp phó học tập, một lớp phó văn thể mĩ từ 45 bạn học sinh lóp 11 A 2 tương ứng với một chỉnh hợp chập 3 của 45 phần tử. Do đó số cách chọn là: \(A_{45}^3\).
+) Chọn 2 bạn làm thư kí từ 42 bạn còn lại. Mỗi cách chọn này không phân biệt về thứ tự nên số cách chọn là: \(C_{42}^2\).
Bước 2. Sử dụng quy tắc nhân.
Công việc được thực hiện hai bước liên tiếp nên theo qui tắc nhân, ta có số cách cô giáo chọn ra một ban cán sự lớp thỏa mãn yêu cầu bài toán là: \(A_{45}^3.C_{42}^2 = 3! \cdot C_{45}^3.C_{42}^2\)
Có bao nhiêu cách xếp 6 học sinh thành một hàng dọc?
Mỗi cách xếp \(6\) học sinh thành một hàng dọc là một hoán vị của \(6\) phần tử.
Vậy có \({P_6} = 6! = 720\) cách xếp 6 học sinh thành một hàng dọc.
Lập được bao nhiêu số tự nhiên có \(3\) chữ số khác nhau chọn từ tập \(A = \left\{ {1;2;3;4;5} \right\}\) sao cho mỗi số lập được luôn có mặt chữ số \(3\).
Gọi số tạo thành có dạng \(x = \overline {abc} \), với \(a\), \(b\), \(c\) đôi một khác nhau và lấy từ \(A\).
Chọn một vị trí \(a,\,\,b\) hoặc \(c\) cho số \(3\) có \(3\) cách chọn.
Chọn hai chữ số khác \(3\) từ \(A\) và sắp xếp vào hai vị trí còn lại của \(x\) có \(A_4^2\) cách chọn
Theo quy tắc nhân có \(3.A_4^2 = 36\) cách chọn
Mỗi cách sắp xếp như trên cho ta một số thỏa yêu cầu.
Vậy có \(36\) số cần tìm.
Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên chẵn có bốn chữ số đôi một khác nhau?
Bước 1 :
Gọi số có 4 chữ số cần lập là \(\overline {abcd} \,\,\left( {0 \le a;b;c;d \le 9;\,\,a \ne 0;\,\,a,b,c,d \in \mathbb{N}} \right)\).
Bước 2 :
+ Số cần lập là số chẵn \( \Rightarrow d \in \left\{ {2;4;6} \right\} \Rightarrow \) Có 3 cách chọn \(d\).
+ Ứng với mỗi cách chọn \(d\) có \(A_5^3 = 60\) cách chọn 3 chữ số \(a,\,\,b,\,\,c\).
Bước 3 :
Áp dụng quy tắc nhân ta có: \(3.60 = 180\) số thỏa mãn.
Trong mặt phẳng cho 5 đường thẳng song song \({a_1},\,\,{a_2},\,\,{a_3},\,\,{a_4},\,\,{a_5}\) và 7 đường thẳng song song với nhau \({b_1},\,\,{b_2},\,\,{b_3},\,\,{b_4},\,\,{b_5},\,\,{b_6},\,\,{b_7}\) đồng thời cắt 5 đường thẳng trên. Tính số hình bình hành tạo nên bởi 12 đường thẳng đã cho
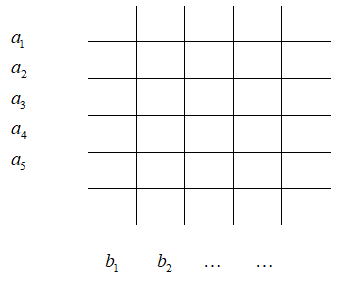
Ta thấy HBH được tạo ra khi chọn 2 đường thẳng a và 2 đường thẳng b
Chọn 2 đường a: \(C_5^2\)
Chọn 2 đường b: \(C_7^2\)
\( \Rightarrow \) \(C_5^2\) \( \times \) \(C_7^2\)
Đề thi THPT QG 2020 – mã đề 104
Có bao nhiêu cách xếp 8 học sinh thành một hàng dọc?
Số cách xếp 8 học sinh thành một hàng dọc là: \(8! = 40320.\)
Số các cách xếp chỗ cho \(n\) người thành một hàng ngang là:
Mỗi cách xếp chỗ cho \(n\) người thành một hàng ngang là một hoán vị của \(n\) phần tử.
Vậy số cách xếp là \({P_n} = n!\)
Số các hoán vị của \(17\) phần tử là:
Số các hoán vị khác nhau của \(17\) phần tử là \(17!\).
Trong tủ sách có tất cả \(10\) cuốn sách được đánh số tử \(1\) đến \(10\). Hỏi có bao nhiêu cách sắp xếp sao cho quyển thứ nhất ở kề quyển thứ hai:
Gom \(2\) quyển sách thứ nhất và thứ hai thành \(1\) quyển nên coi như lúc này chỉ có \(9\) quyển sách.
Hoán vị hai quyển sách có \(2! = 2\) cách.
Sắp \(9\) quyển sách (trong đó có bộ \(2\) quyển sách vừa gom) vào \(9\) vị trí, có \(9!\) cách.
Vậy có \(2.9! = 725760\) cách.
Chọn công thức KHÔNG đúng khi tính số chỉnh hợp chập \(k\) của \(n\) phần tử.
Số chỉnh hợp chập \(k\) của \(n\) phần tử là:
$A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}} = n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - k + 1} \right)$
Do đó A và C đúng, B sai.
Công thức D cũng đúng vì \(\dfrac{{\left( {n + 1} \right)!}}{{\left( {n + 1} \right)\left( {n - k} \right)!}} = \dfrac{{\left( {n + 1} \right)n!}}{{\left( {n + 1} \right)\left( {n - k} \right)!}} = \dfrac{{n!}}{{\left( {n - k} \right)!}}\).
Số các véc tơ (khác \(\overrightarrow 0 \)) được tạo thành từ \(10\) điểm phân biệt trong mặt phẳng là:
Mỗi véc tơ được tạo thành thỏa mãn bài toán ứng với một chỉnh hợp chập \(2\) của \(10\) phần tử.
Vậy số véc tơ là \(A_{10}^2\).
Từ \(7\) chữ số \(1,\,2,\,3,\,4,\,5,\,6,\,7\) có thể lập được bao nhiêu số từ \(4\) chữ số khác nhau?
Chọn \(4\) trong \(7\) chữ số để sắp vào \(4\) vị trí (phân biệt thứ tự) có \(A_7^4 = \dfrac{{7!}}{{3!}} = 7.6.5.4\).
Số tập hợp con gồm \(7\) phần tử của tập hợp \(B\) gồm \(18\) phần tử là:
Mỗi tập con gồm \(7\) phần tử trong tập hợp gồm \(18\) phần tử ứng với một cách chọn \(7\) trong số \(18\) phần tử không phân biệt thứ tự hay chính là một tổ hợp chập \(7\) của \(18\).
Vậy số tập hợp cần tìm là \(C_{18}^7\).
Số tổ hợp chập \(9\) của \(9\) phần tử là:
Số tổ hợp chập \(9\) của \(9\) phần tử là \(C_9^9\).
Trong một hộp bánh có \(6\) loại bánh nhân thịt và \(4\) loại bánh nhân đậu xanh. Có bao nhiêu cách lấy ra \(6\) bánh để phát cho các em thiếu nhi.
Chọn \(6\) trong \(10\) bánh có \(C_{10}^6 = 210\) cách.
Số các hoán vị khác nhau của \(n\) phần tử là:
Số các hoán vị khác nhau của \(n\) phần tử là \({P_n} = n!\)
Số các hoán vị của \(10\) phần tử là:
Số các hoán vị khác nhau của \(10\) phần tử là \({P_{10}} = 10!\).
Có bao nhiêu số có \(5\) chữ số đôi một khác nhau tạo thành từ các chữ số \(1,2,3,4,5\)?
Gọi số thỏa mãn bài toán là: \(\overline {abcde} \).
Mỗi số có \(5\) chữ số thỏa mãn bài toán là một hoán vị của \(5\) chữ số trên.
Số các số là \(5! = 120\) (số).
Số chỉnh hợp chập \(k\) của \(n\) phần tử là:
Số chỉnh hợp chập \(k\) của \(n\) phần tử là:
$A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}} = n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - k + 1} \right)$
Số chỉnh hợp chập \(5\) của \(9\) phần tử là:
Số chỉnh hợp chập \(5\) của \(9\) phần tử là \(A_9^5\).

